Question

A motorboat is racing towards the north at $36km/h$ with respect to water and the speed of water current in that region is $10km/h$ towards east. The resultant speed of the boat is nearly

& A.37m/s \\\ & B.37km/h \\\ & C.46km/h \\\ & D.26km/h \\\ \end{aligned}$$

Answer 1

Since the boat is moving on a river, which is flowing, then we can say that the velocity of the river acts as a hindrance for the movement of the boat. For the boat to cross the river, clearly it must overcome the velocity of the river. Then, we can calculate the resultant vector, from the parallelogram law of vector addition.
Formula used: $v_{r}=\sqrt{v_{b}^{2}+v_{w}^{2}}$

Complete step-by-step solution:
Let us consider that boat starts from a point $O$ as shown in the figure. Let the velocity of the boat be $v_{b}=36km/h$ and the velocity of the $v_{w}=10km/h$.
Let us say that the boat from $O$ reaches the perpendicular point $A$ in the absence of the $v_{w}$. Due to the velocity of the river, $v_{w}$, clearly, this hinders the movement of the boat and thus the boat from $O$ reaches $B$, instead of $A$, which is inclined at an angle $\theta$ with respect to $O\; A$

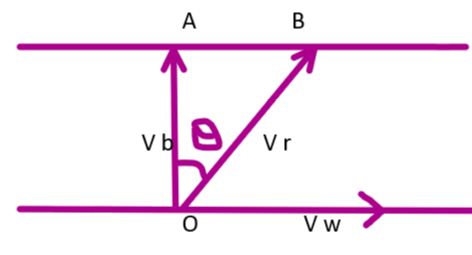
Let $v_{r}$ be the resultant vector. Then from the parallelogram law of vector addition, we can say that figure we can say that the resultant velocity $v_{r}$. Then the magnitude of the resultant vector is given as $v_{r}=\sqrt{v_{b}^{2}+v_{w}^{2}}$
$\implies v_{r}=\sqrt{{36}^{2}+{10}^{2}}=\sqrt{1296+100}=\sqrt{1390}=37.36km/h$
Then, we can say that the value of $v_{r}\approx 37km/h$
Then the direction of the resultant force is given by $\theta=tan^{-1}\dfrac{v_{w}}{v_{r}}$
Substituting, we get, $\theta=tan^{-1}\dfrac{36}{10}=tan^{-1}3.6$
Thus the answer is $B.37km/h$

Note: This sum may seem very hard at first glance, but if one draws the diagram and labels the diagram correctly, it is easy to solve the question. The question uses only the basic parallelogram law of vector addition. Also the direction of the resultant force is given by $\theta=tan^{-1}\dfrac{v_{w}}{v_{r}}$, the direction is not asked here.