Solveeit Logo
Login

Question

Question: A motorboat is observed to travel \(10km{{h}^{-1}}\) relative to the earth in the direction \({{37}^...

A motorboat is observed to travel 10kmh−110km{{h}^{-1}} relative to the earth in the direction 37∘{{37}^{\circ }} north of east. If the velocity of the boat due to the wind only is 2kmh−12km{{h}^{-1}} westward and that due to the current only is 4kmh−14km{{h}^{-1}} southward, what is the magnitude and direction of the velocity of the boat due to its own power?

Explanation

Solution

First draw a schematic diagram showing the data given in the question. The component of velocity in the north of east is resolved into two components. That is, the cosine component along the horizontal direction and the vertical component along vertical direction. Then calculate the resultant velocity in the horizontal and vertical direction and then find the net velocity.

Complete answer:

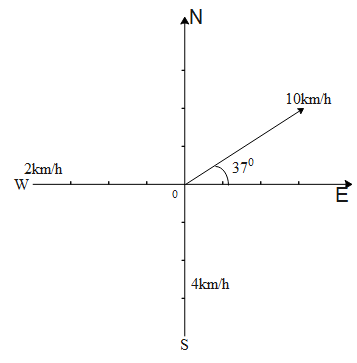
Since the motorboat travels 10kmh−110km{{h}^{-1}}relative to the earth in the direction 37∘{{37}^{\circ }}north of east. The velocity component splits into horizontal and vertical components here. This is shown in the figure below.

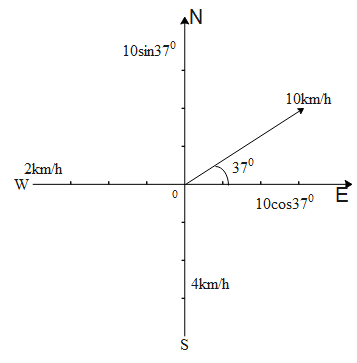
10cos⁡37∘=7.896≃8km/h10\cos {{37}^{\circ }}=7.896\simeq 8km/h
10sin⁡37∘=6.018km/h≃6km/h10\sin {{37}^{\circ }}=6.018km/h\simeq 6km/h
Then the vertical velocity =6−4=2kmh−1=6-4=2km{{h}^{-1}}
Similarly,
The horizontal velocity=8−2=6kmh−1=8-2=6km{{h}^{-1}}
Thus net velocity can be described as the square of the horizontal and vertical velocity.
Hence, the net velocity,
Vnet=22+62  \begin{aligned} & {{V}_{net}}=\sqrt{{{2}^{2}}+{{6}^{2}}} \\\ & \\\ \end{aligned}
⇒Vnet=4+36 ⇒Vnet=40 ∴Vnet=210kmh−1 \begin{aligned} & \Rightarrow {{V}_{net}}=\sqrt{4+36} \\\ & \Rightarrow {{V}_{net}}=\sqrt{40} \\\ & \therefore {{V}_{net}}=2\sqrt{10}km{{h}^{-1}} \\\ \end{aligned}

Additional information:
The motion of one object with respect to the other is known as a relative motion. Here one object is assumed to be fixed while the other is in relative motion. Thus net velocity can be described as the square of the horizontal and vertical velocity.

Note:
The motion of one object with respect to the other is known as a relative motion. Here one object is assumed to be fixed while the other is in relative motion. For any vector we can resolve them into two components. That is, horizontal and vertical components. The horizontal component is usually taken as sine component and vertical component is taken as cosine. Thus net velocity can be described as the square of the horizontal and vertical velocity.