Question

A motor van weighing 4400kg rounds a level curve of radius 200m on an unbanked road at $60kmh{{r}^{-1}}$. What should be the minimum value of coefficient of friction to prevent skidding?

Answer 1

Any motion along a circular track requires a balancing force to keep the motion intact. For motor driving, the velocity has to be controlled in maintaining the centripetal force due to the circular track. The friction offered by the road is added to balancing the centripetal force.

Complete answer:
A road on which the automobiles travel provides sufficient friction for safe travel. On a straight road, the friction allows the tyres to rotate and make possible the rolling motion. This is not the case when we are driving along a curved track. Along the curved path, there is an extra force which is acting towards the center of the circle, i.e., the centripetal force. A component of friction force along the opposite direction enables the car to move safely without skidding.
The roads with very sharp curves are usually banked to increase normal components to balance the centripetal force at even higher velocities. The banking of roads is the process by which the road is built with an angle with the horizontal along the width of the road.
Now let us consider the present situation. It is given that the road is unbanked.

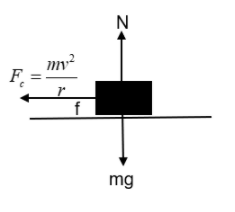
The diagram shows a car moving a turn of radius ‘r’ with a velocity ‘v’. The frictional force is denoted by ‘f’ and the centripetal force as ${{F}_{c}}$.
We know that the frictional force is given as –
$f=\mu N$
The centripetal force is given as –
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$
We know that the car should move without skidding to a maximum when both the forces are equal.
i.e.,

& \dfrac{m{{v}^{2}}}{r}=\mu N \\\ & \Rightarrow \text{ }\mu =\dfrac{m{{v}^{2}}}{Nr} \\\ & \text{Given,} \\\ & m=4400kg, \\\ & v=60kmh{{r}^{-1}}=60\times \dfrac{5}{18}m{{s}^{-1}}=16.67m{{s}^{-1}}, \\\ & r=200m, \\\ & g=10m{{s}^{-2}} \\\ & N=mg \\\ & \Rightarrow \text{ }\mu =\dfrac{4400\times {{(\dfrac{50}{3})}^{2}}}{4400\times 10\times 200} \\\ & \Rightarrow \text{ }\mu =0.14 \\\ \end{aligned}$$ The coefficient of friction required to balance the centripetal force for a safe drive is 0.14. Additional Information: On a banked road, with this coefficient of friction, the car can travel at a higher velocity. **Note:** The coefficient of friction required for a banked road will be lesser than the unbanked road. Because a component of the normal force all acts opposite to the centripetal force and thus contributes in avoiding skidding on the same road. On a banked road, with this coefficient of friction, the car can travel at a higher velocity.