Solveeit Logo
Login

Question

Question: A motor car is going due north at a speed of 50 km/hr. It makes a \({90^0}\)left turn without changi...

A motor car is going due north at a speed of 50 km/hr. It makes a 900{90^0}left turn without changing the speed. The change in the velocity of the car is about
(a) 502 km/hr (b) 70 km/hr (c) 80 km/hr (d) zero  (a){\text{ 50}}\sqrt 2 {\text{ km/hr}} \\\ (b){\text{ 70 km/hr}} \\\ (c){\text{ 80 km/hr}} \\\ (d){\text{ zero}} \\\

Explanation

Solution

Hint: Speed is a scalar quantity as it only has magnitude whereas velocity has both the magnitude as well as direction thus it is a vector. As the car has made a left turn this means the velocity gets changed and this change in velocity is the difference between the final and the initial velocity.

Complete step-by-step answer:

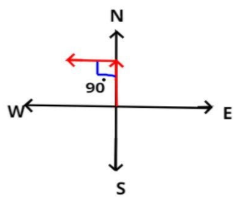
It is given that the motor car is going north at a speed of 50 km/hr. as shown in figure.
So the initial velocity (v) of the car is = 50i^50\hat i km/hr, as (i^)\left( {\hat i} \right) denotes the north direction.
Now the motor car makes a 90 degree left turn as shown in figure so the direction of the motor car is changed to west as shown in figure but it is given that the speed of motor car remains same, so the final velocity (u) of motor car is equal to 50j^50\hat j km/hr, as (j^)\left( {\hat j} \right) denotes the west direction.
Now we have to find out the change in velocity.
So as we know change in velocity is the subtraction of initial velocity (v) to the final velocity (u).
Therefore change in velocity (Vc) = initial velocity – final velocity.
⇒Vc=v−u\Rightarrow {V_c} = v - u
⇒Vc=\Rightarrow {V_c} = 50i^50\hat i km/hr – 50j^50\hat j km/hr =(50i^−50j^) = \left( {50\hat i - 50\hat j} \right) km/hr.
So we have to calculate the magnitude of this change in velocity.
⇒∣Vc∣=∣50i^−50j^∣=(50)2+(50)2=502\Rightarrow \left| {{V_c}} \right| = \left| {50\hat i - 50\hat j} \right| = \sqrt {{{\left( {50} \right)}^2} + {{\left( {50} \right)}^2}} = 50\sqrt 2
So this is the required change in velocity.
Hence option (a) is correct.

Note: Whenever we face such types of problems it is advised to make a simple diagrammatic plot of the directions in which the car moves as it helps understanding the concept of velocity. Sometimes in more complex problems the component of vectors of velocity helps solve the problems.