Question

A motor boat going downstream overcame a raft at a point A. $\tau = 60$ min. Later it turns back and after some time it passes a raft again at a distance $I = 6$ km from point A. Find the flow of velocity assuming the speed of the boat is constant.

Answer 1

Here, first assume the given velocities of the motor and the river flow. Then convert the word statement in the mathematical expressions. Find the relation between the known and unknown terms and solve accordingly as per the required solution.

Complete step by step answer:

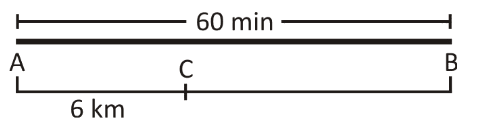
Let us consider that the velocity of the flow of the river is $= {v_f}$. The velocity of the motor boat is $= {v_m}$. When the boat travels in the downstream, then the total velocity of the boat moving in downward stream is $= {v_m} + {v_f}$. When the boat is returning back, the flow of the river would be in the opposite direction. So, the total velocity of the moving boat is $= {v_m} - {v_f}$

Referring to the given diagram, the motor boat starts its journey from point A and reaches at point B after travelling for $60$ minutes or $1$ hour. Boat returns back and travels for time “t” and reaches a point C. So, the total time taken is $(1 + t)$ hours for $6$ km.
$v{}_f(1 + t) = 6{\text{ }}....{\text{ (a)}}$
Now, the net displacement from the point A to the point C is $6{\text{ km}}{\text{.}}$ we can expressed as follows-
$\left( {{v_m} + {v_f}} \right)\left( 1 \right) + \left[ { - ({v_m} - {v_f})(t)} \right] = 6$
Simplify the above equation –
${v_m} + {v_f} - {v_m}t + {v_f}t = 6$
Take like terms together –
${v_f}(1 + t) + {v_m} - {v_m}t = 6$
Place value in the above equation from the equation (a)
$6 + {v_m} - {v_m}t = 6$
Like terms with the same value and same sign cancel each other from both the sides of the equation. So, remove “$6$ “ from both sides.
${v_m} = {v_m}t$

Like terms with the same value and same sign cancel each other from both the sides of the equation. So, remove “${v_m}$ “ from both sides.
$1 = t \\\ \Rightarrow t = 1{\text{ hr}} \\\$
Now, place the value of time “t” in equation (a)
$\Rightarrow v{}_f(1 + 1) = 6{\text{ }}$
Simplify and make the subject ${v_f}$
$\Rightarrow {v_f}(2) = 6 \\\ \Rightarrow {v_f} = \dfrac{6}{2} \\\ \therefore {v_f} = 3km/hr \\\$
Thus, the flow of the velocity is $3km/hr$.

Note: Here, the given word statement should be converted in the correct and proper mathematical expression carefully. First few steps are very important in this question. Follow the given data carefully and solve applying basic velocity relations.