Question

A motor boat going downstream crosses a float at a point A. 60 minutes later it turns back and after some time it again crosses the float, now the float is at a distance of 12 km from the point A. The velocity of the stream is:
A. $6km/h$
B. $3km/h$
C. $4km/h$
D. $2km/h$

Answer 1

Students need to have a clear understanding of relative velocity and linear equations. The crucial point to realize in this question is that the time taken by float to cover 12 km is equal to the time taken by the motorboat to reach the float again after it turned and travelled upstream. Also, it would be helpful if they draw a figure to try and understand the motion of the boat and the float.

Complete step by step solution:
First, we will assume that the velocity of boat = $V$
Also, another assumption will be velocity of stream = $v$
To understand this question, we’ll draw a figure. Let $AB$ be the total distance covered by the motorboat from point $A$ in 60 minutes. Also, let $C$ be the point where the motorboat and the float meet again.
Let $t$ be the time taken by the boat to reach $C$ after turning at the point $B$ .
At the beginning, it is given that the Float is at point $A$ .

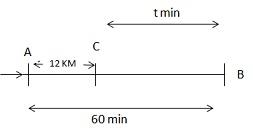
Then, according to the question, Float covers $AC$ distance in $(t + 60)$ min.
Hence, the Boat covers $BC$ distance in $t$ min
So,
$v(t + 60) = 12 \to (1) \\\ (v + V)60 = AB \to (2) \\\ (V - v)t = BC = AB - 12 \to (3) \\\$
Solving equation (1), (2) and (3) we get $t = 60$ minutes.
From this,
$v(120) = 12 \\\ v = 0.1km/\min = 0.1 \times 60km/h = 6km/h \\\$
Thus, the velocity of the stream comes out to be $6km/h$ , and option A is correct.

Note:
There can be two cases of an object in motion when in a stream/river/canal. Either the body can flow upstream (in that case the velocity of the stream is subtracted from the velocity of the object), or it can flow downstream (in this case, the velocity of the stream is added to the velocity of the object).