Question

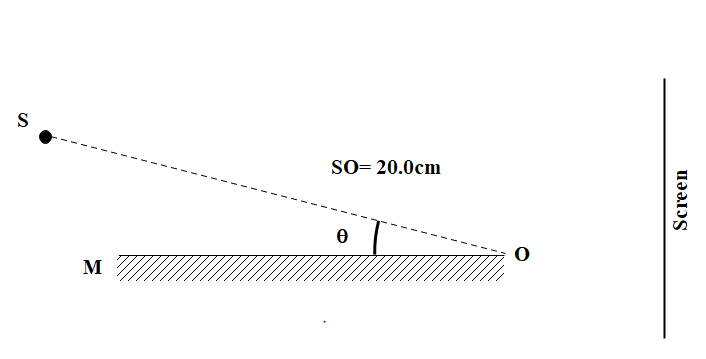
A monochromatic light source S of wavelength 440 nm is placed slightly above a plane mirror M as shown. Image of S in M can be used as a virtual source to produce interference fringes on the screen. The distance of source S from O is 20.0cm, and the distance of screen from O is 100.0 cm (figure is not to scale). If the angle $\theta = 0.50 \times {10^{ - 2}}$ radians, the width of the interference fringes observed on the screen is?

A. 2.20 mm
B. 2.64mm
C. 1.10 mm
D. 0.55 mm

Answer 1

Firstly we will draw the ray diagram to have a clear idea of the question. According to figure ${S_1}$ will behave as a virtual source of light and we will be able to observe Young’s double-slit which has the distance between the source d and distance between the source and the screen is d. We will use the mathematical expressions of this physical phenomenon to find the required answer
Formula used:
$\beta = \dfrac{{\lambda D}}{d}$

Complete answer:
Given in the question are the following:
Wavelength, $\lambda = 44nm = 440 \times {10^{ - 9}}m$
\eqalign{ & SO = 20.0cm \cr & \theta = 0.5 \times {10^{ - 2}}radians \cr}

We can assume the given system to be acting like Young’s double-slit experiment. We need to find the width of the fringes. Let $S$ and ${S_1}$ be the source of light for Young’s double-slit experiment as shown in the figure below:

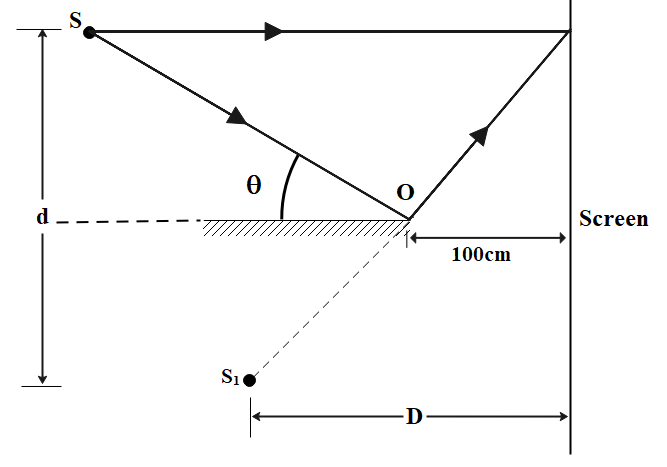
From the diagram, we have:
\eqalign{ & D = SO\cos \theta + 100 \cr & \Rightarrow D = 20 \times 1 + 100 \cr & \therefore D = 120cm \cr}
Similarly,
\eqalign{ & d = 2 \times SO\sin \theta \cr & \Rightarrow d = 2 \times 20 \times 0.5 \times {10^{ - 3}} \cr & \therefore d = 2 \times {10^{ - 2}}cm \cr}
Now, the fridge width in Young’s double slit is given by:
$\beta = \dfrac{{\lambda D}}{d}$
Substituting the calculated values in the above equation we get:
\eqalign{ & \beta = \dfrac{{440 \times {{10}^{ - 6}} \times 120 \times {{10}^2}}}{{2 \times {{10}^{ - 2}} \times {{10}^2}}} \cr & \Rightarrow \beta = 264 \times {10^{ - 2}} \cr & \therefore \beta = 2.64mm \cr}
The width of the interference fringes observed on the screen is 2.64 mm.

So, the correct answer is “Option B”.

Note:
In diffraction slit width matters. When the slits are narrow, any light that passes through them, bends at the corners, hence suffer diffraction. As a result, there is considerable overlap of the diffraction patterns and hence wide fringes are observed. But, if we increase the width of slits then most of the light passes through the slits without undergoing diffraction. Hence there is less diffraction and the fringes become narrow and lesser in number because of the overlap diffraction is less.