Question

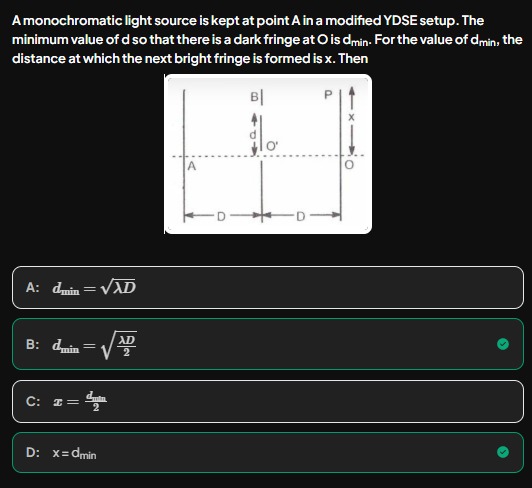
A monochromatic light source is kept at point A in a modified YDSE setup. The minimum value of d so that there is a dark fringe at O is dmin. For the value of dmin, the distance at which the next bright fringe is formed is x. Then

• A. $d_{min} = \sqrt{\lambda D}$
• B. $d_{min} = \sqrt{\frac{\lambda D}{2}}$
• C. $x = \frac{d_{min}}{2}$
• D. $x = d_{min}$

Answer 1

Answer: (B), (D)

Option B (for $d_{min}=\sqrt{\frac{\lambda D}{2}}$) and Option D (for $x=d_{min}$)

Answer 2

1. Extra Illumination phase:

   The lower slit at O′ is at distance D from the source A, while the upper slit B, being at a vertical separation d, is at distance approximately

   $\approx D+\frac{d^2}{2D}$

   so the phase difference due to illumination is

   $\phi_{\rm ill}=\frac{2\pi}{\lambda}\cdot\frac{d^2}{2D}$.

2. Path Difference to the Observation Point O:

   At point O (on the same horizontal through A and O′) the two waves travel different distances. The extra path from B (relative to O′) is also approximately

   $\frac{d^2}{2D}$.

   Thus the phase difference due to propagation is

   $\phi_{\rm prop}=\frac{2\pi}{\lambda}\cdot\frac{d^2}{2D}$.

3. Total Phase Difference at O:

   Adding the two contributions:

   $\phi_{\rm total}=\frac{2\pi}{\lambda}\left(\frac{d^2}{2D}+\frac{d^2}{2D}\right)=\frac{2\pi d^2}{\lambda D}$.

   For a dark fringe at O (destructive interference), we require

   $\frac{2\pi d^2}{\lambda D}=\pi$,

   which gives

   $d^2=\frac{\lambda D}{2}\quad\Longrightarrow\quad d_{\min}=\sqrt{\frac{\lambda D}{2}}$.

   This confirms Option B.

4. Next Bright Fringe:

   As the interference pattern from the two slits is shifted (since the central fringe is dark), the conditions for bright fringes become:

   $\phi_{\rm total}(y)=\frac{2\pi d^2}{\lambda D}-\frac{2\pi d\,y}{\lambda D} =2\pi m$.

   For the next bright fringe (taking m = 1 and noting that at y = 0 we had $\phi=\pi$), one finds after setting up the equation and substituting $d_{\min}$ that

   $x=y=d_{\min}$.

   This confirms Option D.