Solveeit Logo
Login

Question

Question: A monochromatic light is travelling in a medium of refractive index \(n = 1.6\). It enters a stack o...

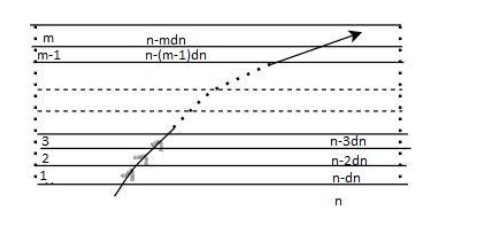
A monochromatic light is travelling in a medium of refractive index n=1.6n = 1.6. It enters a stack of glass layers from the bottom side at an angle θ=30∘\theta = {30^ \circ }. The interfaces of the glass layers are parallel to each other. The refractive indices of the different glass layers are monotonically decreasing as nm=n−mΔn{n_m} = n - m\Delta n, where nm{n_m} is the refractive index of the mth{m^{th}} slab and Δn=0.1\Delta n = 0.1 (see the figure). The ray is refracted out parallel to the interface between the (m−1)th{\left( {m - 1} \right)^{th}} and mth{m^{th}} slabs from the right side of the stack. What is the value of the mm ?

Explanation

Solution

Calculate the value of the nm{n_m} from the relation given in the question. Substitute this value of the refractive index of the slab and also the refractive angles in the snell’s law. The obtained value gives the output of the value of the m constant.

Useful formula:
The snell’s law states that
nsin⁡θ=nmsin⁡θrn\sin \theta = {n_m}\sin {\theta _r}
Where nn is the refractive index, θ\theta is the angle between the layers of the glass and the bottom side an nm{n_m} is the refractive index of the mth{m^{th}} slab.

Complete step by step solution:
It is given that the
nm=n−mΔn{n_m} = n - m\Delta n
Δn=0.1\Delta n = 0.1
n=1.6n = 1.6
From the above given data, the value of nm{n_m} is calculated as follows.
nm=n−mΔn{n_m} = n - m\Delta n
Substituting the values known,
nm=1.6−0.1m{n_m} = 1.6 - 0.1m -------------(1)
By using the snell’s law
1.6sin⁡30∘=nmsin⁡90∘1.6\sin {30^ \circ } = {n_m}\sin 90 \circ
The θr{\theta _r} is observed as 90∘{90^ \circ } from the diagram given. And substitute the value of (1) in the above equation.
1.6sin⁡30∘=(1.6−0.1m)sin⁡90∘1.6\sin {30^ \circ } = (1.6 - 0.1m)\sin 90 \circ
1.62=0.1m×1\dfrac{{1.6}}{2} = 0.1m \times 1
By performing the simple arithmetic operation,
0.1m=0.80.1m = 0.8
m=8m = 8

Thus the value of the mm is 88.

Note: The snell’s law provides the idea about the relationship between the angle of the incidence and the angle of the refraction. This law is also called the law of refraction. The refractive index depends on the layer of the substance that obstructs the flow of the light.