Question

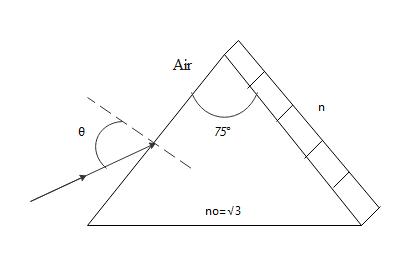
A monochromatic light is incident from air on a refracting surface of a prism of angle ${75^0}$ and refractive index ${n_0} = \sqrt 3$. The other refracting surface of the prism is coated by a thin film of material of refractive index n as shown in figure. The light suffers total internal reflection at the coated prism surface for an incidence angle of θ ≤ ${60^0}$. The value of ${n^2}$ is _______.

Answer 1

Velocity of light will be different in different media. If velocity of light is higher in one medium and lesser in another medium then the first one is called a rarer medium and the second one is called denser medium. There is a law called snell’s law which relates the refractive indices of the media.

Formula used:
${\mu _i}\sin i = {\mu _r}\sin r$
${r_1} + {r_2} = A$

Complete step by step answer:
Velocity is nothing but the rate of change of displacement i.e the ratio of displacement to the time taken. So the time taken will be displacement upon the velocity.
Velocity of light in any medium of refractive index(n) will be
$v = \dfrac{c}{n}$ where ‘c’ is the velocity of light in the free space and ‘n’ is the refractive index of the medium.
For air, the refractive index will be one. For prisms glass refractive index will be greater than one. Hence when light enters from air to glass, its velocity decreases. In order to maintain the same time displacement also must decrease. That means the path travelled in the air by the light must decrease. This will be possible if the light bends towards the normal. Hence the incident angle and the refracted angle will be different. They are related with refractive indices and given by Snell’s law.
${\mu _i}\sin i = {\mu _r}\sin r$
Where ${\mu _i}$ is the refractive index of incident medium and ${\mu _r}$ is the refractive index of refracted medium. $i$ is the incident angle and $r$ is the refracted angle.
The air refractive index is one. The prism and the entire information is given below in the form of a diagram.

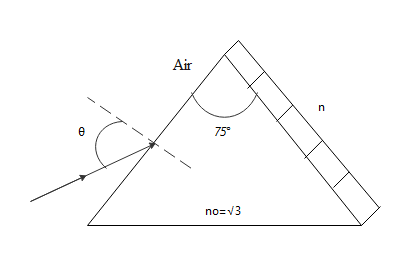
Incident angle $\theta \leqslant {60^0}$. Hence we will consider the limiting case 60 degrees. By applying snell’s law at incident interface we get
${\mu _i}\sin i = {\mu _r}\sin r$
\eqalign{ & \Rightarrow 1\sin 60 = {n_0}\sin {r_1} \cr & \Rightarrow \dfrac{{\sqrt 3 }}{2} = \sqrt 3 \sin {r_1} \cr & \Rightarrow \sin {r_1} = \dfrac{1}{2} \cr & \therefore {r_1} = {30^0} \cr}
We have
${r_1} + {r_2} = A$
\eqalign{ & \Rightarrow 30 + {r_2} = 75 \cr & \therefore {r_2} = {45^0} \cr}
Apply the total internal reflection condition at the other side of the prism and film interface.
${\mu _i}\sin i = {\mu _r}\sin r$
\eqalign{ & \Rightarrow {n_0}\sin {r_2} = n\sin 90 \cr & \Rightarrow \sqrt 3 \sin 45 = n\sin 90 \cr & \Rightarrow n = \sqrt {\dfrac{3}{2}} \cr & \therefore {n^2} = \dfrac{3}{2} \cr}
Thus the above expression gives us the required value of ${n^2}$ .

Note:
After the first refraction from the air and prism surface the refracting angle will be ${r_1}$ and the incident angle at the prism and film interface at the other side will be ${r_2}$. Now the sum of these two angles will be equal to the angle of the prism. By using this information and using critical angle conditions at the prism and film interface, we had found the refractive index of film.