Question

A monochromatic beam of light is incident at $60{}^\circ$ on one face of an equilateral prism of refractive index $n$ and emerges from the opposite face making an angle $\theta$ with the normal. For $n=\sqrt{3}$ the value of $\theta$ is $60{}^\circ$ and $\dfrac{d\theta }{dn}=m$ . The value of $m$ is

Answer 1

Hint : By Snell’s law for refraction, we can find the refraction angle at the first refracting surface. From this, the incidence angle for the second refracting angle can be found. By using the Snell’s Law for the second refracting surface, we can find the value of the required derivative.

Complete Step By Step Answer:
Here, we are given that the monochromatic light is incident to the prism at an angle $60{}^\circ$
The incident light gets refracted at the interface and is deviated to an angle $r_1$ to the normal.
The refracted light travels in the prism and strikes the prism on the opposite side.
The refracted light makes an angle $r_2$ with the normal at the opposite interface and gets refracted when it comes out of the prism as the emergent light which makes an angle $\theta$ with the normal as shown in figure below.

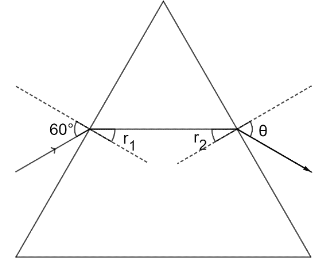
We know that the relation between $r_1$ and $r_2$ can be expressed as
${{r}_{1}}+{{r}_{2}}=A$ , where $A$ is the Angle of Prism
As the prism is equilateral,
$\therefore {{r}_{1}}+{{r}_{2}}=60{}^\circ$ …… $(1)$
Now, the Snell’s Law can be expressed as
${{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}}$
For the first interface with incident light going in,
${{n}_{1}}$ = Refractive index of air = $1$
${{\theta }_{1}}$ = Angle of incidence = $60{}^\circ$
${{n}_{2}}$ = Refractive index of glass = $n$
${{\theta }_{2}}$ = Angle of refraction = $r_1$
Substituting the above values in Snell’s Law,
$(1)\sin (60{}^\circ )=n\sin {{r}_{1}}$
$\therefore n\sin {{r}_{1}}=\dfrac{\sqrt{3}}{2}$ …… $(2)$
Similarly for the second interface with emerging light coming out,
${{n}_{1}}$ = Refractive index of glass = $n$
${{\theta }_{1}}$ = Angle of refraction = $r_2$
${{n}_{2}}$ = Refractive index of air = $n$
${{\theta }_{2}}$ = Angle of emergence = $\theta$
Substituting the above values in Snell’s Law,
$n\sin {{r}_{2}}=(1)\sin\theta$
$\therefore n\sin {{r}_{2}}=\sin \theta$ …… $(3)$
From the equation $(1)$ , we get
${{r}_{2}}=60{}^\circ -{{r}_{1}}$
Substituting in the equation $(3)$ ,
$\therefore n\sin (60{}^\circ -{{r}_{1}})=\sin \theta$
$\therefore n\left( \sin 60{}^\circ \cos {{r}_{1}}-\cos 60{}^\circ \sin {{r}_{1}} \right)=\sin \theta$
Converting cosine in terms of sine and putting the known values of cosine and sine,
$\therefore n\left( \dfrac{\sqrt{3}}{2}\sqrt{1-{{\sin }^{2}}{{r}_{1}}}-\dfrac{1}{2}\sin {{r}_{1}} \right)=\sin \theta$ …… $(4)$
From the equation $(2)$ ,
$\sin {{r}_{1}}=\dfrac{\sqrt{3}}{2n}$
Substituting this value in the equation $(4)$ ,
$\therefore n\left( \dfrac{\sqrt{3}}{2}\sqrt{1-\dfrac{3}{4{{n}^{2}}}}-\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2n} \right)=\sin \theta$
$\therefore n\left( \dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{4{{n}^{2}}-3}}{2n}-\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2n} \right)=\sin \theta$
Canceling out the common terms and taking common terms out of parenthesis,
$\therefore \dfrac{\sqrt{3}}{4}\left( \sqrt{4{{n}^{2}}-3}-1 \right)=\sin \theta$
Now, differentiating on both the sides,
$\therefore \dfrac{\sqrt{3}}{4}\left( \dfrac{1}{2\sqrt{4{{n}^{2}}-3}}\times 8ndn-0 \right)=\cos \theta d\theta$
$\therefore \dfrac{\sqrt{3}n}{\sqrt{4{{n}^{2}}-3}}dn=\cos \theta d\theta$
Substituting the values for the specific condition i.e. $n=\sqrt{3}$ , $\theta =60{}^\circ$
$\therefore \dfrac{\sqrt{3}\times \sqrt{3}}{\sqrt{4{{\left( \sqrt{3} \right)}^{2}}-3}}dn=\cos 60{}^\circ d\theta$
$\therefore \dfrac{3}{3}dn=\dfrac{1}{2}d\theta$
Hence, the value of the derivation,
$\therefore \dfrac{d\theta }{dn}=2$
Thus, the final answer is $m=2$

Note :
Here, we have derived the equation for the derivation in general terms and then substitute the value. Here, we are asked a particular solution for a general derivation. Hence, we cannot directly substitute the value and then find the derivative, as we can only substitute the initial conditions given. If we substitute the values before the derivation, the answer we calculate will be wrong.