Question

A monkey of mass m kg slides down a light rope attached to a fixed spring balance, with an acceleration a. The reading of the spring balance is W kg [g=acceleration due to gravity]
(This question has multiple correct options)
A. the force of friction exerted by the rope on the monkey is $m\left( {g - a} \right)N$
B. $m = \dfrac{{Wg}}{{g - a}}$
C. $m = W\left( {1 + \dfrac{a}{g}} \right)$
D. the tension in the rope is $Wg$ N

Answer 1

If you observe this problem, all the questions are related to force. Hence, these statements can be validated by drawing the free-body diagram for each case and solving for the force.
The free-body diagram is a diagram where the entire mass of the system is represented by a block of mass m and all the forces acting on it are displayed.

Complete step-by-step answer:
Let us analyse each statement and determine whether it is correct or incorrect.
Statement – A: The force of friction exerted by the rope on the monkey is $m\left( {g - a} \right)N$
Let us draw the free-body diagram for a monkey pulling the rope with the friction.

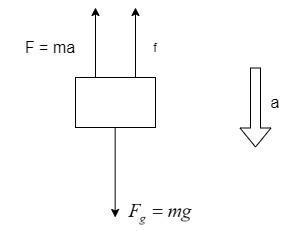
The two forces acting on the monkey of mass m are: Weight acting downwards, ${F_g} = mg$and frictional force acting on the rope, which is in the opposite direction of the weight.
In the free-body diagram, if the acceleration is acting, a force equal to the mass of the body times the acceleration should be considered as acting in the opposite direction of the acceleration, as shown above.
Equating the forces, we get –
${F_g} = F + f$
$\Rightarrow mg = ma + f$
From the above equation, the friction,
$f = mg - ma = m\left( {g - a} \right)$
Hence, this statement is correct.
Statement – B: $m = \dfrac{{Wg}}{{g - a}}$
When the spring is pulled by a mass of W g, there is tension acting on the spring, equal to the mass reading of the spring balance and the acceleration due to gravity.
Tension in spring, $T = Wg$
where W is the reading of the spring balance.
Drawing the free-body diagram involving the tension,

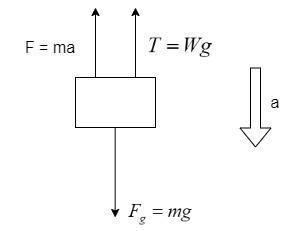
Here, only the weight ${F_g}$ is acting downwards and the acceleration of the body, and the tension on the spring is $T = Wg$
In the free-body diagram, if the acceleration is acting, a force equal to the mass of the body times the acceleration should be considered as acting in the opposite direction of the acceleration, as shown above.
Equating the forces, we get –
$F + T = {F_g}$
$\Rightarrow ma + Wg = mg$
Rearranging, we get –
$Wg = mg - ma$
$\Rightarrow Wg = m\left( {g - a} \right)$
$\Rightarrow m = \dfrac{{Wg}}{{g - a}}$
Hence, this statement is correct.
Statement – C: $m = W\left( {1 + \dfrac{a}{g}} \right)$
Let us solve the given equation in the statement to verify its authenticity.
$m = W\left( {1 + \dfrac{a}{g}} \right)$
$\Rightarrow m = W\left( {\dfrac{{g + a}}{g}} \right)$
$\Rightarrow m = W\left( {\dfrac{{g + a}}{g}} \right) \ne \dfrac{{Wg}}{{g - a}}$
Since the expression does not match the true statement, Statement-B, this equation is not correct.
Hence, this statement is incorrect.
Statement – D: The tension in the rope is $Wg$ N
When the spring is pulled by a mass of W g, there is tension acting on the spring, equal to the mass reading of the spring balance and the acceleration due to gravity.
Tension in spring, $T = Wg$newtons (N)
where W is the reading of the spring balance.
Thus, tension, $T = Wg$ N.
Hence, this statement is correct.

From all the above 4 statements, Statement A, B and D are correct.

Note: The tension in the spring developed due to the weight is responsible for restoring the original configuration of the spring, also known, as the restoring force.
The restoring force is directly proportional to the displacement of the spring.
Restoring force, $F \propto x$
$F = kx = T$
where k is called the spring constant.