Question

A monkey of mass $m$ climbs a rope slung over a light frictionless pulley. The opposite end of the rope is tied to a block of mass $M$ lying on a smooth horizontal plane. Then the acceleration of block when monkey moves upwards with an acceleration $'a'$ relative to rope is

Answer 1

When the monkey is climbing up on the rope. The rope will be sliding down because of the weight of the monkey. Therefore, there will be an acceleration of the monkey and the acceleration of the rope. The relative acceleration is the vector difference of these two accelerations. Use the concept of relative acceleration to calculate the acceleration of monkeys.

Complete step by step answer: Observe the diagram:

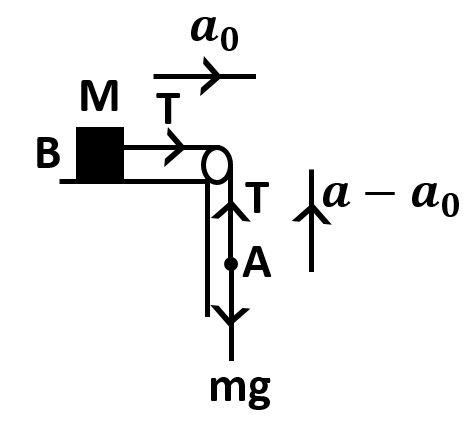
Let point A be the position of monkey.
Let the mass of the monkey be $m$
Let the acceleration of monkey be ${a_m}$
Let point B is the position of the block
The mass of the block is $M$
When the monkey would climb up, the force exerted by the monkey to go up will cause the block to move. Let the acceleration of the block be ${a_0}$
Acceleration of the block will be the acceleration of the rope as the block will move with the rope.
Let the acceleration in the rope be ${a_r}$
$\Rightarrow {a_r} = {a_0}$
Let the acceleration of the monkey relative to the rope be ${a_{mr}}$
According to the concept of relative motion,
${a_{mr}} = {a_m} - {a_r}$ . . . (1)
It is given to us that the relative acceleration of the monkey with respect to the rope is $a$
$\Rightarrow {a_{mr}} = a$
Therefore, from equation (1), we get
$a = {a_m} - ( - {a_0})$ $\left( {\because {a_r} = {a_0}} \right)$ . . . (2)
$a = {a_m} + {a_0}$
Rearranging it we can write
${a_m} = a - {a_0}$
Force applied is given by
$F = ma$
Where,
$F$ is force applied
$m$ is mass of the body
$a$ is acceleration of the body
Now, we know that the force exerted on the block B is equal to the tension applied on the rope.
$\Rightarrow F = M{a_0} = T$ . . . (3)
Where,
$T$ is tension on the rope.
Using the same concept, we can say that the force applied on the monkey due to the acceleration ${a_m}$ is equal to the difference of tension on the rope and the weight of the monkey.
Let ${F_m}$ be the force with which the monkey is accelerating upwards.
$\Rightarrow {F_m} = T - mg = m{a_m}$
$\Rightarrow T - mg = m(a - {a_0})$ $\left( {\because {a_m} = a - {a_0}} \right)$
Rearranging it we can write
$T = m(a - {a_0}) + mg$ . . . (4)
Comparing the values of $T$ from equation (3) and equation (4), we can write
$M{a_0} = m(a - {a_0}) + mg$
Rearranging it we can write
$M{a_0} = ma - m{a_0} + mg$
$\Rightarrow M{a_0} + m{a_0} = ma + mg$
$\Rightarrow (M + m){a_0} = m(a + g)$
$\Rightarrow {a_0} = \dfrac{{m(a + g)}}{{(M + m)}}$
Therefore, from the above explanation, we can conclude that the acceleration of the block is ${a_0} = \dfrac{{m(a + g)}}{{(M + m)}}$

Note: Acceleration, force, tension etc are vector quantities, using them need the use of their magnitude as well as direction. We cannot use one and not the other. In this question, we have considered all the quantities moving up to be positive and all the quantities moving from left to right to be positive. Therefore, the acceleration of rope at point A, in equation (2), is negative as the rope is accelerating downwards.