Question

A monkey of mass $20kg$ is holding a vertical rope. The rope will not break when a mass of $25kg$ is suspended from it but will break if the mass exceeds $25kg$. What is the maximum acceleration with which the monkey can climb up along the rope (in $m/{{s}^{2}}$)
A) 2.5
B) 10
C) 12
D) 15

Answer 1

We will use the force block diagram method, to find the acceleration of the climbing of the monkey, First we need the tension formed on the string when the monkey climbs and the opposite force to counter the tension that will be the force exerted by the monkey when climbing the rope. The tension in this case will also be known as breaking force as the mass given in the question is the mass before breaking, if extra weight is exerted hence tension will be the product of breaking mass with the gravitational force. Let us describe a formula that tells us the force relationship between the monkey and the rope:
$T=ma+mg$
where $T$ is the tension or the breaking force, $m$ is the mass of the monkey, $a$ is the acceleration with which the monkey is climbing and $g=10m/{{\sec }^{2}}$ .

Complete step by step solution:
The weight of the monkey climbing the rope is given as $20kg$.
The breaking weight of the rope or the mass upon exceeding the rope will break is $25kg$.
The acceleration with which the monkey climbs the rope is $a\text{ }m{{s}^{-2}}$.
Now let us draw a diagram to portray how the monkey and the rope are exerting force on one-another.

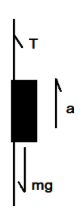
Now according to the diagram drawn below the relation between the tension (breaking force) on the rope, monkey and the acceleration of the monkey is:
$T=ma+mg$
Placing the value of the mass $m=20kg$ as the mass of the monkey and for the value of $T$, the tension calculated has the mass $25kg$ which is the breaking weight.
$\Rightarrow 25\times 10=20a+20\times 10$
$\Rightarrow a=\dfrac{25\times 10-20\times 10}{20}$
$\Rightarrow a=2.5m/{{\sec }^{2}}$
Therefore, the acceleration due to monkeys moving upward is $a=2.5m/{{\sec }^{2}}$.

Note: Another method to solve the question is by finding the extra weight that is left before the rope breaks. The difference between weights of the monkey and the breaking weight is $25kg-20kg=5kg$. Making the total force as $5kg\times 10m/{{\sec }^{2}}$, where $10m/{{\sec }^{2}}$ is the gravity and equating this force with the force with which monkey climbs as:
$5kg\times 10m/{{\sec }^{2}}=ma$ (mass of the monkey is $20kg$)
$\Rightarrow 5kg\times 10m/{{\sec }^{2}}=20a$
$\Rightarrow a=\dfrac{5kg\times 10m/{{\sec }^{2}}}{20}$
$\Rightarrow a=2.5\text{ }m/{{\sec }^{2}}$