Question

A monkey is climbing up a tree at a speed of $3{\text{m}}{{\text{s}}^{ - 1}}$. A dog runs towards the tree with a speed of ${\text{4m}}{{\text{s}}^{ - 1}}$. Find the relative speed of the dog as seen by the monkey.
A. ${\text{7m}}{{\text{s}}^{ - 1}}$
B. ${\text{5m}}{{\text{s}}^{ - 1}}$
C. ${\text{ < 5m}}{{\text{s}}^{ - 1}}$
D. Between ${\text{5m}}{{\text{s}}^{ - 1}}$ and ${\text{7m}}{{\text{s}}^{ - 1}}$

Answer 1

Here if the tree is considered to exist in the first quadrant, then the velocity of the monkey is directed along the positive y-axis and the velocity of the dog is directed along the positive x-axis. So the two velocities are perpendicular to each other. So the velocity of the dog with respect to the monkey will be the difference between these two velocities.

Formula used:
$\to$The velocity of an object 1 with respect to object 2 is given by, ${\vec v_{1/2}} = {\vec v_1} - {\vec v_2}$ where ${\vec v_1}$ is the velocity of object 1 and ${\vec v_2}$ is the velocity of object 2.

Complete step-by-step solution:
$\to$Step 1: List the parameters known from the question.
The magnitude of the velocity of the monkey is given to be ${v_m} = 3{\text{m}}{{\text{s}}^{ - 1}}$ . Then in vector representation, it will be ${\vec v_m} = 3\hat j$ .
The magnitude of the velocity of the dog is given to be ${v_d} = 4{\text{m}}{{\text{s}}^{ - 1}}$ . Then in vector representation, it will be ${\vec v_d} = 4\hat i$ .

$\to$Step 2: Express the velocity of the dog as seen by the monkey.
The relative velocity of the dog is given by, ${\vec v_{dm}} = {\vec v_d} - {\vec v_m}$ ------- (1)
Substituting for ${\vec v_m} = 3\hat j$ and ${\vec v_d} = 4\hat i$ in equation (1) we get, ${\vec v_{dm}} = 4\hat i - 3\hat j$
Then the magnitude of the relative velocity will be ${v_{dm}} = \sqrt {{4^2} + {3^2}} = \sqrt {25} = 5{\text{m}}{{\text{s}}^{ - 1}}$
Thus the velocity of the dog as observed by the monkey is $5{\text{m}}{{\text{s}}^{ - 1}}$.

So the correct option is B.

Note:-
Alternate method-
Since the given velocities of the monkey and dog are perpendicular to each other, they can be viewed as the height $a$ and base $b$ of a right-angled triangle whose hypotenuse $c$ will be the velocity of the dog as seen by the monkey. The figure depicting this right triangle is given below.

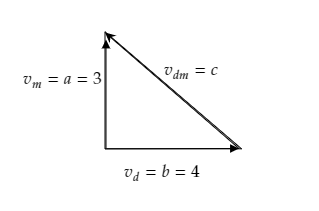
Then from Pythagoras theorem, we have ${c^2} = {a^2} + {b^2}$ .
Substituting for $a = 3$ and $b = 4$ in the above relation we have ${c^2} = {3^2} + {4^2} = 25$
$\Rightarrow c = \sqrt {25} = 5$
Hence the velocity of the dog as observed by the monkey will be $5{\text{m}}{{\text{s}}^{ - 1}}$