Question

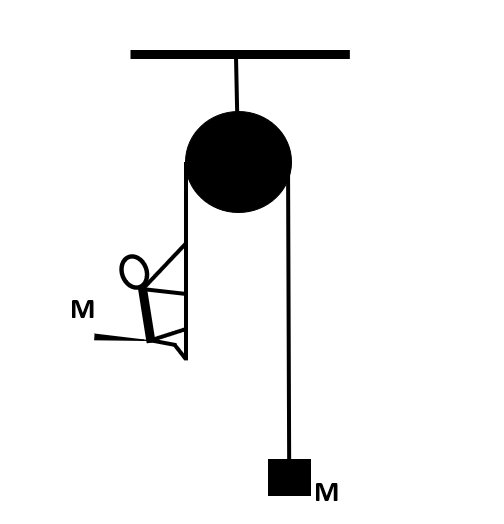
A monkey is climbing on a rope that goes over a smooth light pulley and supports a block of equal mass at the other end. Show that whatever force the monkey exerts on the rope, the monkey and the block move with the same acceleration.

Answer 1

We will initially assume the acceleration of monkey and block to be unequal and in the opposite direction. Then, we will write the force equation for monkey and the block, so that we get the values of these accelerations. Only after this, we would be able to comment on their acceleration with respect to each other.

Complete answer:
Since, the mass of the monkey and the block are the same. Let them be equal to ‘M’. Also, let the tension in the string be denoted by T. Assuming an ideal string, the tension will be the same at every part of the string.
Now, let the acceleration of the monkey be ‘a’ upwards and let the acceleration of the block be ‘b’ downwards. Now, writing the force equation on the monkey and the block, we have:
The force equation on monkey can be written as:
$\Rightarrow T-Mg=Ma$
$\Rightarrow a=\dfrac{T-Mg}{M}$ [Let this expression be equation number (1)]
Now, writing the force equation on the block, we have:
$\Rightarrow Mg-T=Mb$
$\Rightarrow b=\dfrac{Mg-T}{M}$ [Let this expression be equation number (2)]
On dividing equation number (2) by equation number (1), we get:
$\begin{aligned} & \Rightarrow \dfrac{b}{a}=\dfrac{\dfrac{Mg-T}{M}}{\dfrac{T-Mg}{M}} \\\ & \Rightarrow \dfrac{b}{a}=-1 \\\ & \therefore b=-a \\\ \end{aligned}$
Hence, from the above relation between the accelerations of the monkey and the block, we can clearly say that both, the monkey and the block have the same acceleration irrespective of how much force the monkey exerts on the rope.

Note:
At every time (t), the block and the monkey will move with the same acceleration. That is, if they are at rest, no motion occurs as they are of the same mass. And if afterwards, the monkey starts pulling the rope, their separation will still remain constant due to equal accelerations.