Question

A mirror $\left( {\mu = \dfrac{3}{2}} \right)$ is $10cm$ thick. An object is placed $15cm$ in front of it. The position of image from the front surface is:
(A) $15cm$
(B) $21.67cm$
(C) $28.34cm$
(D) $35cm$

Answer 1

Hint : To solve this question, we need to use the concept of apparent shift. We will first find the apparent distance of the image from the mirror. Then we will find the actual distance of the image from the front surface using the apparent distance.

Complete Step By Step Answer:
Let us first draw the diagram of the given situation.

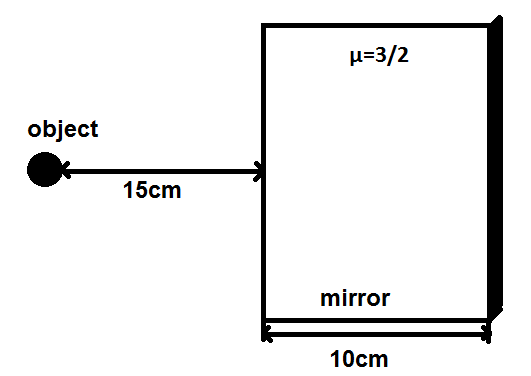
Now, if we consider the apparent shift, the object is to be appeared as it has moved toward the mirror by the distance of $t\left( {1 - \dfrac{1}{\mu }} \right)$ , where $t$ is the thickness of mirror and we are given $t = 10cm$ .
$t\left( {1 - \dfrac{1}{\mu }} \right) = 10\left( {1 - \dfrac{1}{{\dfrac{3}{2}}}} \right) = 10\left( {1 - \dfrac{2}{3}} \right) = \dfrac{{10}}{3}cm$
Therefore, the apparent distance of the image from the mirror will be $15 + 10 - \dfrac{{10}}{3} = \dfrac{{65}}{3}cm$ .
Therefore, the formation of the image will take place at $\dfrac{{65}}{3}cm$ behind the mirror.
When we look at the image from the opposite side of the mirror, it will again shift towards the mirror by $\dfrac{{10}}{3}cm$ .
Therefore, the apparent distance will be $\dfrac{{65}}{3} - \dfrac{{10}}{3} = \dfrac{{55}}{3}cm$ .
Thus, the distance of the final image from the front surface will be This apparent distance plus the thickness of the mirror which is $\dfrac{{55}}{3} + 10 = \dfrac{{85}}{3} = 28.34cm$ .
Hence, option C is the right answer.

Note :
In this question, the main point to consider is the apparent shift. It is defined as the perpendicular distance between the incident and the emergent ray with reference to refraction of light through a glass slab. Here, we have considered the mirror as the glass slab.