Question

A mirror is inclined at an angle $\theta$with the horizontal. If a ray of light is incident on the mirror at an angle$\theta$, then the reflected ray makes the following angle with the horizontal:
A) $\theta$
B) $2\theta$
C) $\dfrac{\theta }{2}$
D) ${90^ \circ }$

Answer 1

In this question, we need to determine the angle made by the reflected ray with the horizontal. Here we will use the concept of law of Reflection which states that “When light is reflected from a surface then the angle of incidence is always equal to the angle of reflection, incidence angle and the reflected angle is measured from the path of the light to the normal to the surface to point at which light strikes this is known as law of reflection”.

Complete step by step answer:
Let AB be the mirror inclined at an angle $\theta$ with the plane AM
Now a ray of light $\overrightarrow {PQ}$ is incident at an angle $\theta$ on the plane mirror AB, we know Snell’s law states that when a light is incident on a plane mirror at an angle $\theta$ then the light will be reflected by making an angle $\theta$.
Hence we can say $\overrightarrow {QR}$ the reflected ray will also make an angle $\theta$
Now draw a line XY normal to the mirror AB, therefore we can say
$\angle PQX = \angle RQX$

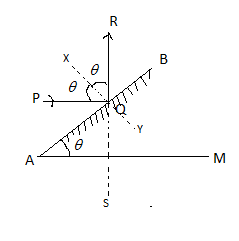
Now extend back the reflected ray $\overrightarrow {QR}$to the surface AM at point S.
Since $\angle RQB = {90^ \circ } - \theta$
$\therefore \angle AQS = {90^ \circ } - \theta$[By law of reflection]
Now in $\vartriangle AQS$
$\angle QAS = \theta$
$\angle AQS = {90^ \circ } - \theta$
As we know the total internal angle of a triangle is equal to${180^ \circ }$, therefore in the $\vartriangle AQS$

$$\angle QAS + \angle AQS + \angle QSA = {180^ \circ } \\\ \Rightarrow \theta + {90^ \circ } - \theta + \angle QSA = {180^ \circ } \\\ \Rightarrow \angle QSA = {90^ \circ } \\\$$

Hence the reflected ray makes an angle ${90^ \circ }$ with the horizontal AM
Option D is correct.

Note: Students must be careful while using the angle of incidence and the reflection as we have to always take only similar angles that are either made with the horizontal or the vertical.