Question
Question: A minute particle resting at a frictionless surface is acted upon by a constant horizontal force. Ne...
A minute particle resting at a frictionless surface is acted upon by a constant horizontal force. Neglecting frictional force the graph between work done on the particle W and speed of particle u is represented by:
(A)
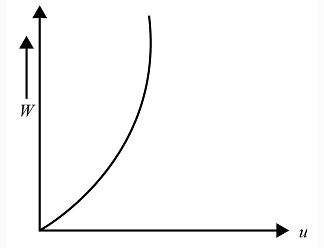
(B)
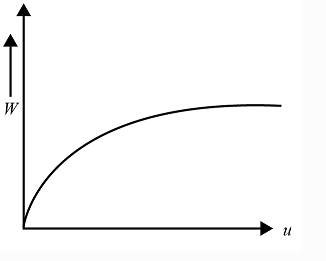
(C)
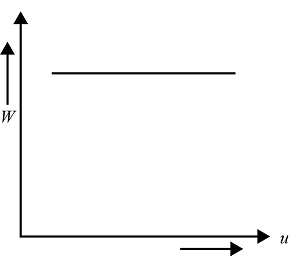
(D)
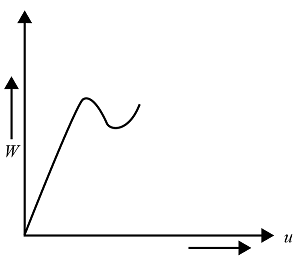
Solution
Hint : In order to solve this question, we are going to look at the relation between the velocity and the work from the work- energy theorem, and analyze which type of the equation it is, and then, check from the options that which one best matches the equation for the velocity and the work relation.
According to the work-energy theorem
W=21mu2
Where, m is the mass of the particle and v is the velocity with which it is moving
The equation of a parabola is y2=4ax
Complete Step By Step Answer:
According to the work-energy theorem,
The work done on a system can be converted to the energy of the system is
W=21mu2
Where, m is the mass of the particle and v is the velocity with which it is moving
The equation can also be written as
⇒u2=m2W
This equation resembles the equation of a parabola
i.e. y2=4ax
Thus, the graph between the work done on the particle W and the speed of the particle u must resemble with the graph for a parabolic curve
Out of the four options, a parabolic equation is the best represented by option (A)
i.e.
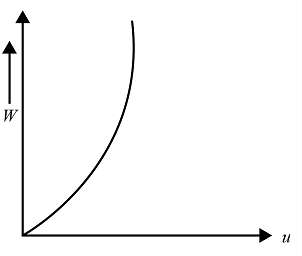
Hence, option (A) is the correct answer.
Note :
The principle for the work-energy theorem states that the work done by all the forces acting on a particle equals the change in the kinetic energy of the particle. In this case, the initial velocity hence, kinetic energy is zero. So, only the final kinetic energy of the particle i.e. 21mu2 is used there.
