Question
Question: A millimetre of range \[10\text{ }mA\]and resistance\[~9\Omega \] is joined in a circuit as shown in...
A millimetre of range 10 mAand resistance 9Ω is joined in a circuit as shown in figure. The meter gives full-scale deflection for current I when Aand Bare used as its terminals. If current enters atA and leaves atB (C is left isolated), the value of I is
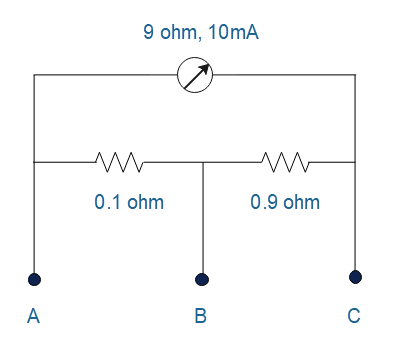
A. 100mAB. 900mAC. 1AD. 1.1A
Solution
Hint: C is isolated i.e. no current flows from branch C. Use Kirchhoff’s current law to calculate current in each of the branches and then Kirchhoff’s voltage law to calculate voltage in each of the terminals. Using KCL, find current in each of the branches. This is how you will get voltage in each of the branches.
Formula used:
V=IR
Where,
V=VoltageI= CurrentR= Resistance
Complete step by step answer:
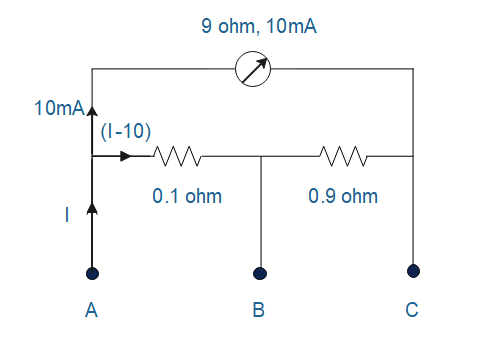
In the question it is given that the meter gives full-scale deflection for current Iwhen A and Bare used as its terminals. Cis isolated.
Branch Cis detached now.
LetIbe the current flowing through Abranch, shown in figure. IfIbe the current entering through A and 10mAis the current flowing through 9Ω then remaining current flowing through 0.1Ωis(I−10).
Since Cis isolated therefore the circuit will look as follows
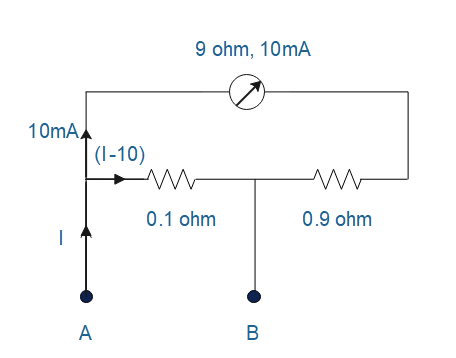
From the figure we can say that resistance9Ωand 0.9Ωare in series now and series combinations of these two resistance are in parallel with0.1Ωresistance.
We know that if two branches are in parallel then potential in both the branches is the same.
Therefore we can write as
