Question

A middle C string on a piano has a fundamental frequency of 262 Hz and the A note has a fundamental frequency of 440 Hz.
(a) Calculate the frequencies of the next two harmonics of the C string.
(b) If the strings for the A and C notes are assumed to have the same mass per unit length and the same length determine the ratio of tensions in the two strings.

Answer 1

For part (a): Frequency of harmonics string is an integral multiple of fundamental frequency. Using this relation, the frequency of the next two harmonics can be calculated. For part (b): Use Mersenne Equation showing relation between fundamental frequency and amount of tension on the string. Substitute value in this equation for both the fundamental frequencies and take their ratio.

Formula used: $F= \dfrac {1}{2L} \sqrt {\dfrac {T}{\mu}}$

Complete step by step answer:

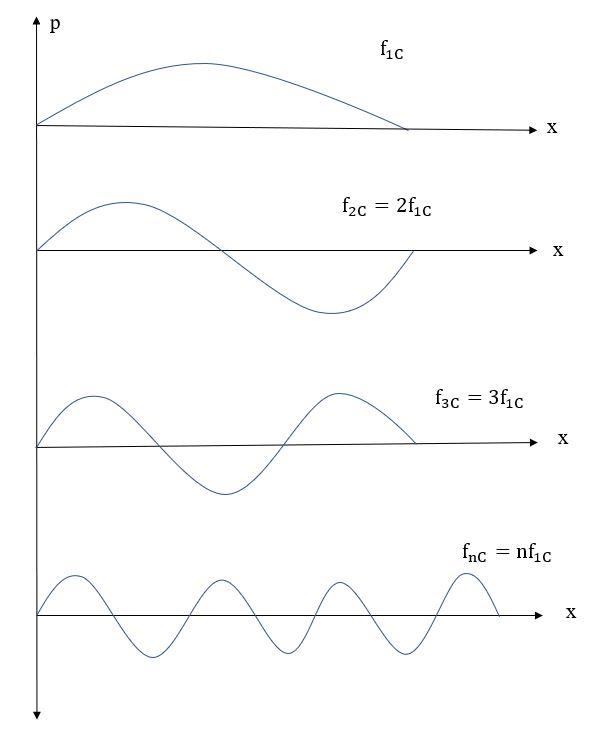
Given: ${f}_{1C} = 262 Hz$
A. Let the frequencies of next two harmonics of the C string be ${f}_{2C}$ and ${f}_{3C}$
${f}_{2C}=2 \times {f}_{1C}$
$\therefore {f}_{2C}= 2\times 262$
$\therefore {f}_{2C}= 524 Hz$
Now, ${f}_{3C}=3 \times {f}_{1C}$
$\therefore {f}_{3C}= 3\times 262$
$\therefore {f}_{2C}= 786 Hz$

Hence, the next two harmonics of C strongly have frequencies of 524 Hz and 786 Hz.

B. We know,
$F= \dfrac {1}{2L} \sqrt {\dfrac {T}{\mu}}$
Where, F is the fundamental frequency
T is the tension on the string
L is the length of the string
$\mu$ is the mass per unit length
Now, using the above formula we write the expressions for both the fundamental frequencies.
${f}_{1A}= \dfrac {1}{2L} \sqrt {\dfrac {{T}_{A}}{\mu}}$ ...(1)
${f}_{1C}= \dfrac {1}{2L} \sqrt {\dfrac {{T}_{C}}{\mu}}$ ...(2)
Now, dividing the equation. (1) by (2) we get,
$\dfrac {{f}_{1A}}{{f}_{1C}}= \sqrt {\dfrac {{T}_{A}}{{T}_{C}}}$
Now substituting the values for frequencies we get,
$\sqrt {\dfrac {{T}_{A}}{{T}_{C}}}=\dfrac {440}{226}$
$\therefore \sqrt {\dfrac {{T}_{A}}{{T}_{C}}}= 1.68$
Then, squaring on both the sides we get,
$\dfrac {{T}_{A}}{{T}_{C}}= {1.68}^{2}$
$\therefore \dfrac {{T}_{A}}{{T}_{C}}=2.82$

Hence, the ratio of tension in two strings is 2.82.

Note: Always remember that the harmonics of a string have frequencies related to the integral multiple of the fundamental frequency. In reality, frequency of piano strings does not depend on tension on the string. It depends on many other parameters such as length of the string, mass per unit length etc.