Question

A metre stick is balanced on a knife-edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?

Answer 1

A body is said to be in rotational equilibrium when the net torque acting on the body is equal to zero. Thus, in rotational equilibrium, the body will be either at rest or will be moving at a constant angular velocity.
$\sum T = 0$
Centre of mass is the point on a body where the entire mass of the body acts on.

Complete step by step solution:
When the metre scale is completed unloaded, the centre of mass of the metre scale will be at the 50 cm mark.

But, when a weight is added on either side of the 50 cm mark, the centre of mass shifts and the support must be moved to a different point such that, at this point, the sum of moments on either side of the support are equal, resulting in rotational equilibrium.

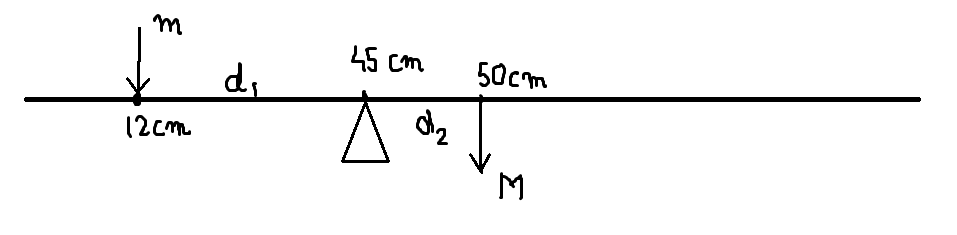
In the problem, it is stated that adding 2 coins at the 12 cm mark will result in shifting of the support to 45 cm from the 50 cm mark.
Mass of coins added, $m = 2 \times 5 = 10g$
Distance at which coins are placed from the new support, ${d_1} = 45 - 12 = 33cm$
Distance of the centre of mass from the new support, ${d_2} = 50 - 45 = 5cm$
Mass of the scale, M =?
To determine the mass of the scale, we should use the balancing of moments.
Moment due to the coins, ${\tau _1} = m \times {d_1}$
Moment due to the mass of the scale, ${\tau _2} = M \times {d_2}$
For equilibrium –
${\tau _1} = {\tau _2} \\\ m \times {d_1} = M \times {d_2}$
Substituting,
$10 \times 33 = M \times 5$
Solving,
$M = \left( {\dfrac{{10 \times 33}}{5}} \right) = \left( {\dfrac{{330}}{5}} \right) = 66g \\\$

$\therefore$ Mass of the scale = 66 g

Note:
Moment of force and torque have the same definition yet, they are not the same conceptually. Both are products of force and distance but, it is the characteristic that each of the quantities is associated with, makes the difference between them.
Moment of force is associated with Bending across the body while Torque is associated with Twisting along the axis of the body.