Question

A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
(A) 13 g
(B) 33 g
(C) 66 g
(D) 99 g

Answer 1

In this problem initially before placing the two additional coins the metre stick as the name suggests its length is 100 cm was balanced at its centre. It is clear its centre of mass is at its geometrical centre. Now after placing two additional coins but not at its geometrical centre, its equilibrium gets disturbed and feels a torque.

Complete step by step answer:

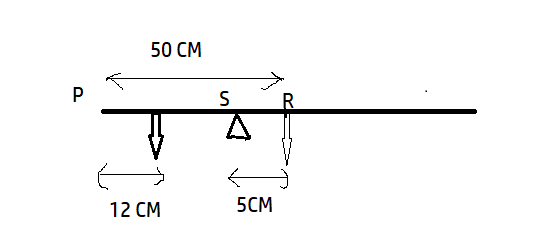
Let W and W’ be the respective weights of the metre stick and the coin.
We do not know the mass of the metre stick. So, let us assume it be m.
Mass of one coin= 5g
Mass of two coin= 10g= 0.01kg
the coins are placed 12cm away from the end P as it can be seen in the figure above. The coins are placed at a distance of 45 cm from the centre of mass which is also the axis of rotation in this case, see the figure above. Now new balancing point is found to be at 45.0 cm. Using rotational equilibrium, we get,
torque due to the weight of two coins= torque due to the centre of mass of the stick
torque is given as $\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}$
for both of the torques the angle between the force which is weight and perpendicular distance from axis of rotation is ${{90}^{0}}$. Thus, $\tau =rF$

& 10g(45-12)=mg(50-45) \\\ & 330=5 \\\ & m=66g \\\ \end{aligned}$$ Hence, the weight of the metre stick is 66g. Thus, the correct option is (C) **Note:** While calculating torque we have to keep in our mind that it is a vector quantity and is given by the cross product of force acting on the body and the perpendicular distance from the axis of rotation. So we have to consider the angle between the two vectors.