Question

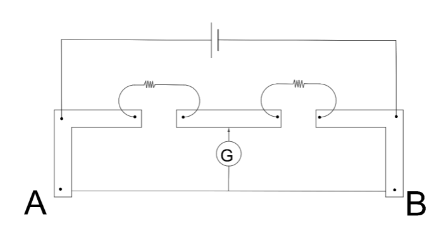
A meter bridge set up as shown to determine end correction at $A$ and $B$. When a resistance of $15{\text{ }}\Omega$ is used in left gap and of $20{\text{ }}\Omega$ in right gap, then null point comes at a distance $42{\text{ }}cm$ from $A$. When these resistance are interchanged, the null point comes at a distance $57{\text{ }}cm$ from $A$.Values of end correction are:

A. $1{\text{ }}cm$, $2{\text{ }}cm\:$
B. $2{\text{ }}cm$, $3{\text{ }}cm\:$
C. $3{\text{ }}cm$, $4{\text{ }}cm\:$
D. $3{\text{ }}cm$, $2{\text{ }}cm\:$

Answer 1

Firstly, we will use the idea of Wheatstone bridge principle. Then, we will take into consideration our concept of end correction. Finally, we will form equations for end corrections in each case and then solve the equations and evaluate the required answers.

Formula Used:
$\dfrac{R}{S}{\text{ }} = \dfrac{{L{\text{ }} + {\text{ }}\alpha }}{{100{\text{ }} - {\text{ }}L{\text{ }} + \beta }}$

Complete step by step answer:
The null point of a meter bridge is the point on the wire where the ratio of resistances connected in the gap becomes proportional to the ratio of the lengths of the pin of the meter bridge from either side of the bridge. When this happens, there is no current flowing through the galvanometer and thus the name null point. For the first case, we have
$R{\text{ }} = {\text{ }}15{\text{ }}\Omega$
$\Rightarrow S{\text{ }} = {\text{ }}20{\text{ }}\Omega$
$\Rightarrow L{\text{ }} = {\text{ }}42{\text{ }}cm$
Thus, putting these values in the formula for the Wheatstone bridge, we get
$\dfrac{{15}}{{20}}{\text{ }} = {\text{ }}\dfrac{{42{\text{ }} + {\text{ }}\alpha }}{{58{\text{ }} + {\text{ }}\beta }}$

Cross multiplying, we get
$15{\text{ }}(58{\text{ }} + {\text{ }}\beta ){\text{ }} = {\text{ }}20{\text{ }}(42{\text{ }} + {\text{ }}\alpha )$
Then, the equation turns out to be
$870{\text{ }} + {\text{ }}15\beta {\text{ }} = {\text{ }}840{\text{ }} + {\text{ }}20\alpha$
Thus, we have the equation as
$20\alpha {\text{ }} - {\text{ }}15\beta {\text{ }} = {\text{ }}30{\text{ }} - - - - - - - - - - - - - {\text{ }}(i)$
Now, for the second case,
$R{\text{ }} = {\text{ }}20{\text{ }}\Omega$
$\Rightarrow S{\text{ }} = {\text{ }}15{\text{ }}\Omega$
$\Rightarrow L{\text{ }} = {\text{ }}57{\text{ }}cm$
Thus, putting in the values in the formula for Wheatstone bridge, we get
$\dfrac{{20}}{{15}}{\text{ }} = {\text{ }}\dfrac{{57{\text{ }} + {\text{ }}\alpha }}{{43{\text{ }} + {\text{ }}\beta }}$
Further, we get
$20{\text{ }}(43{\text{ }} + {\text{ }}\beta ){\text{ }} = {\text{ }}15{\text{ }}(57{\text{ }} + {\text{ }}\alpha )$
Then, we get
$860{\text{ }} + {\text{ }}20\beta {\text{ }} = {\text{ }}855{\text{ }} + {\text{ }}15\alpha$
Further, we get
$15\alpha {\text{ }} - {\text{ }}20\beta {\text{ }} = {\text{ }}5{\text{ }} - - - - - - - - - - - - - - - - - - - {\text{ }}(ii)$

Now, evaluating $3{\text{ }} \times {\text{ }}(i){\text{ }} - {\text{ }}4{\text{ }} \times {\text{ }}(ii)$, we get
$60\alpha {\text{ }} - {\text{ }}45\beta {\text{ }} - {\text{ }}60\alpha {\text{ }} + {\text{ }}80\beta {\text{ }} = {\text{ }}90{\text{ }} - {\text{ }}20$
Thus, we get
$35\beta {\text{ }} = {\text{ }}70$
Evaluating further, we get
$\beta {\text{ }} = {\text{ }}2$
Substituting these values in equation $(i)$, we get
$20\alpha {\text{ }} - {\text{ }}15{\text{ }} \times {\text{ }}2{\text{ }} = {\text{ }}30$
Further, we get
$20\alpha {\text{ }} - {\text{ }}30{\text{ }} = {\text{ }}30$
Then, we have
$20\alpha {\text{ }} = {\text{ }}60$
Thus, we get
$\therefore \alpha {\text{ }} = {\text{ }}3$
Hence, the end corrections are $2{\text{ }}cm$, $3{\text{ }}cm$.

Thus, the correct option is B.

Note: Students often commit errors while solving the equations as they select a method where they fall into some clumsy calculations leading them eventually to the wrong answer. Students should keep in mind that the end correction is a necessary parameter in getting accurate and precise observations keeping the practical side of the meter bridge.