Question

A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm

Answer 1

In this question, we first need to find the volume of the metallic spherical shell using the formula $\dfrac{\pi }{6}\left( {{D}^{3}}-{{d}^{3}} \right)$. Then equate this volume to the volume of the cone with given conditions as it is being melted and being recast which is given by the formula $\dfrac{1}{3}\pi {{r}^{2}}h$. Now, on simplifying it further we get the value of the height of the cone.

Complete step by step answer:**
HOLLOW SPHERE(SHELL):
The solid enclosed between two concentric is called a hollow sphere
The volume of hollow sphere is given by the formula
$\dfrac{\pi }{6}\left( {{D}^{3}}-{{d}^{3}} \right)$

RIGHT CIRCULAR CONE:
A right circular cone is a solid generated by revolving of a right angled triangle through one of its sides (other than hypotenuse) containing the right angle as an axis.
The volume of a cone is given by the formula
$\dfrac{1}{3}\pi {{r}^{2}}h$
Let us assume the volume of spherical shell as V and volume of cone as v also assume that diameters of hollow sphere as D, d and radius of cone as r and height of cone as h
Let us first find the volume of the hollow sphere using the formula
$V=\dfrac{\pi }{6}\left( {{D}^{3}}-{{d}^{3}} \right)$
Now, form the given conditions in the question we have
$D=8,d=4$

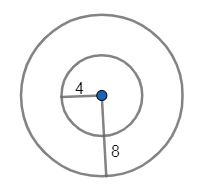
Now, on substituting these values in the above formula we get,
$\Rightarrow V=\dfrac{\pi }{6}\left( {{8}^{3}}-{{4}^{3}} \right)$
Now, this can be further written in the simplified form as
$\Rightarrow V=\dfrac{\pi }{6}\left( 512-64 \right)$
Now, on further simplification we get,
$\therefore V=\dfrac{224\pi }{3}$
Let us now find the volume of the cone with the given conditions
$r=\dfrac{8}{2}=4$

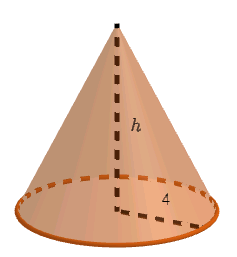
Now, on substituting the respective values in the formula we get,
$\Rightarrow v=\dfrac{1}{3}\pi {{4}^{2}}h$
Here, as hollow sphere is being melted and re casted in to cone we have
$\Rightarrow v=V$
Now, on substituting the respective values we get,
$\Rightarrow \dfrac{1}{3}\pi {{4}^{2}}h=\dfrac{224\pi }{3}$
Let us now cancel the common terms on both the sides
$\Rightarrow 16h=224$
Let us now divide with 16 on both the sides
$\Rightarrow h=\dfrac{224}{16}$
Now, on further simplification we get,
$\therefore h=14cm$
Hence, the correct option is (b).

Note:**
Instead of finding the volumes of each hollow sphere and cone separately and then equating them we can also solve it by first equating the volumes and then consider the respective formulae and substitute the respective values and simplify further.
It is important to note that we can either choose the volume of the hollow sphere formula in terms of radius or diameter but as given in the question we need to choose accordingly.
It is also to be noted that given the base diameter of the cone so when substituting the value in the question we first need to find the corresponding value of radius and then substitute that value because substituting value of diameter in radius gives incorrect result.