Question

A metallic sphere weighing 3kg in air is held by a string so as to be completely immersed in a liquid of relative density 0.8. The relative density of the metallic sphere is 10. The tension in the string is
$A.$ 18.7 N
$B.$ 42.5 N
$C.$ 32.7 N
$D.$ 27.6 N

Answer 1

We need to equate all the forces acting on the metallic sphere. In this question there are three forces acting in the ball namely; the tension of the string, the buoyancy force due to the liquid and the weight of the sphere itself. We need to analyze the direction of each force before substituting into the equation. For example, tension in the string and the buoyant force acts upwards and the weight of the body acts downwards.

Complete answer:
We can find the tension in the string by equating the forces acting downwards and upwards. The summation of the forces will be zero as they are in equilibrium.
Values that are given to us are
Weight: $m=3$kg
Density of the liquid: $\rho =0.8$
Relative density of the metallic sphere: $\sigma =10$
Tension of the string: T
Let us consider gravitational force to be $g=10\dfrac{m}{{{s}^{2}}}$.

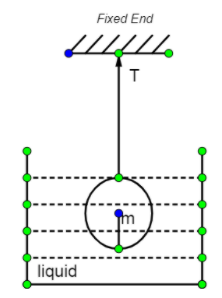
For the system to be in equilibrium
$T+{{F}_{a}}=$Weight
Here,
$\Rightarrow {{F}_{a}}=\rho \times V\times g$(Where ${{F}_{a}}$ is the buoyant force)
Weight= $\sigma \times V\times g$
So now,
$\Rightarrow T=V\times g\times \rho \times [1-(\dfrac{\sigma }{\rho })]$
$\Rightarrow T=m\times g\times [1-(\dfrac{\sigma }{\rho })]$ (Since$m=V\times \rho$)
Now let us substitute the values in the above equation
$\Rightarrow T=3\times 10\times [1-(\dfrac{0.8}{10})]$
$\Rightarrow T=30\times 0.92$
$\Rightarrow T=27.6N$

Hence the correct option is D.

Note:
Equilibrium is the state of a system in which all the forces are balanced. The buoyant force acting on the sphere is due to the liquid displaced by it when it is completely immersed in the liquid. The force is directly proportional to the weight of the liquid displaced by it. For this system to be in equilibrium, the weight of the sphere should be equal to the summation of the tension of the string and the buoyant force.