Question

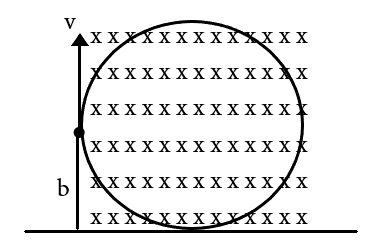
A metallic sheet is placed with its face parallel to the magnetic induction $B$ of a uniform magnetic field. A particle of mass $m$ and charge $q$ is projected with a velocity $v$ from a distance $d$ from the plane normal to the lines of induction. Then the maximum velocity of projection for which the particle does not hit the plane is

(A) $\dfrac{{2qBd}}{m}$
(B) $\dfrac{{qBd}}{m}$
(C) $\dfrac{{qBd}}{{2m}}$
(D) $\dfrac{{qBm}}{{2d}}$

Answer 1

Hint : The centripetal acceleration is provided by the magnetic force on the charge. For the particle to not touch the plane, the radius must be less than the distance. So by equating the formulas for the force experienced by a particle in a magnetic field and the centripetal force, we can calculate the answer.

Formula used: In this solution we will be using the following formula;
$\Rightarrow {F_c} = \dfrac{{m{v^2}}}{r}$ where ${F_c}$ is the centripetal force, $m$ is the mass of a circulating body, $v$ is the speed of rotation and $r$ is the radius of the circle completed by the object.
$\Rightarrow {F_B} = qvB\sin \theta$ where ${F_B}$ is the magnetic force on a body, $q$ is the charge of the body, $B$ is the magnetic field, and $\theta$ is the angle between velocity $\theta$ and $B$ .

Complete step by step answer
A charge moving in a magnetic field experiences a force given by,
$\Rightarrow {F_B} = qvB\sin \theta$ where ${F_B}$ is the magnetic force on a body, $q$ is the charge of the body, $B$ is the magnetic field, and $\theta$ is the angle between velocity $\theta$ and $B$ .
In the case of our charge in the question, it is said to be normal to the surface, hence, $\theta = 90^\circ$
Thus, the magnitude of the force becomes
$\Rightarrow {F_B} = qvB\sin 90^\circ = qvB$ (since $\sin 90^\circ = 1$ )
A body moving into a magnetic field circulates into a circle, and continually moves as such. The centripetal force requires to continue circular motion is given as
$\Rightarrow {F_c} = \dfrac{{m{v^2}}}{r}$ where ${F_c}$ is the centripetal force, $m$ is the mass of a circulating body, $v$ is the speed of rotation and $r$ is the radius of the circle completed by the object.
But this centripetal force must be force must be provided by the magnetic force, hence,
$\Rightarrow qvB = \dfrac{{m{v^2}}}{r}$
Multiplying both sides by $r$ and dividing both sides by $mv$ , we have
$\Rightarrow v = \dfrac{{qrB}}{m}$ , hence, for which the particle must not hit the plane, we say that
$\Rightarrow r < d$ , hence
$\Rightarrow v < \dfrac{{qdB}}{m}$ , hence
$\therefore {v_{\max }} = \dfrac{{qBd}}{m}$
Thus, the correct option is B.

Note
In actuality, at this ${v_{\max }}$ , the projectile will just touch the plane (neglecting all other forces and interactions). The real maximum velocity should be any velocity just under (even infinitesimally) this calculated maximum velocity. However, because velocity is continuous and thus can take any value, thus the velocity infinitesimally close (but not exactly it) would also not touch the plane, hence we choose ${v_{\max }}$ to be the maximum velocity.