Question

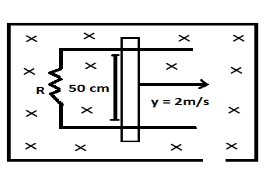
A metallic rod completes its circuit as shown in the figure. The circuit is normal to the magnetic field of $B=0.15tesla$. If the resistance of the rod is $3 ohm$. Find the force required to move the rod with a constant velocity of $2m/sec$?
A. $3.75 \times {10^{ - 3}}N$
B. $3.75 \times {10^{ - 2}}N$
C. $3.75 \times {10^2}N$
D. $3.75 \times {10^{ - 4}}N$

Answer 1

To find the sufficient external to move the rod in the magnetic field with a velocity of $2m/sec$ , we can use faraday's law which states that induced emf is equal to the rate of change of magnetic field flux. When an electrical conductor is introduced into a magnetic field, due to its dynamic interaction with the magnetic field, emf is induced in it. This emf is known as induced emf.

Complete step by step answer:

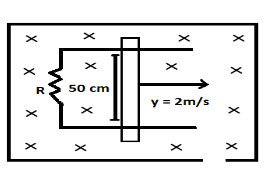
The metallic rod is given to be placed in electric field
Its Induced emf (e) can be given as: Magnetic field density (B) $\times$ velocity (v) $\times$ length of the rod (l).
$e=B \times v \times l$
The magnetic field and resistance are given to be 0.15 Tesla and 3 ohm respectively. substituting the values, we get:
$e = 0.15 \times 2 \times 0.5 \\\ \Rightarrow e = 0.15{\text{ }}v \\\$
So the induced emf is 0.15 volts .
Now with this information we can find the current in the circuit using the formula for current:
$I = \dfrac{{emf}}{{res\left( \Omega \right)}}{\text{ }}\left( {from{\text{ }}V = IR} \right)$

Where I is the induced current.
i = \dfrac{{0.15}}{3} \\\ \Rightarrow i = 0.05A \\\
We have found out the induced current we can calculate the magnetic force using the formula:
${F_m} = iBl$
Substituting the known values, we get:
${F_m} = 0.05 \times 0.15 \times 0.5$
$\Rightarrow{F_m} = 3.75 \times {10^{ - 3}}N$
By overcoming this force we will be able to move in the opposite direction with a constant velocity of 2m/sec.
So our exterior force should be
$\therefore{F_{ext}} = 3.75 \times {10^{ - 3}} \\\$
Therefore, the force required to move the rod with a constant velocity of 2m/sec is $3.75 \times {10^{ - 3}}N$ and A is the correct option.

Note: The (×) sign in the diagram represents that the direction of the magnetic field is in inward direction from the plane and to show the outward direction we use the symbol ( ° ).Emf is nothing but the voltage only for the circuit. To analyze the direction of the induced current always use the Lorentz hand rule which states that if the thumb of the right hand points along the direction of current, then the remaining curled fingers of the same hand give the direction of the magnetic field due to the current.