Question
Question: A metallic right circular cone of 20 cm height whose vertical angle is \(60^\circ \) is cut in two p...
A metallic right circular cone of 20 cm height whose vertical angle is 60∘ is cut in two parts at needed of its height by a plane parallel to its base. If frustum so obtained be drawn into a wire of diameter 151cm, find length of wire.
Solution
Here in the above question we are talking about the right circular cone.
First we will make frustum from the above given information.
We will cut the cone parallel to base.
Then by using trigonometric ratios we will find some dimensions and then final calculation for that we will equate both the volumes as wire is made from frustum.
We will take wire as a cylindrical figure. With its length as the height of the cylinder.
Formula used
Volume of cone =3πr2H
Volume of frustum =3πh(r12+r22+r1r2)
Volume of cylinder =πr2H′
Complete step by step solution :
Let OCD be the given cone, and ABCD to the required frustum.
.
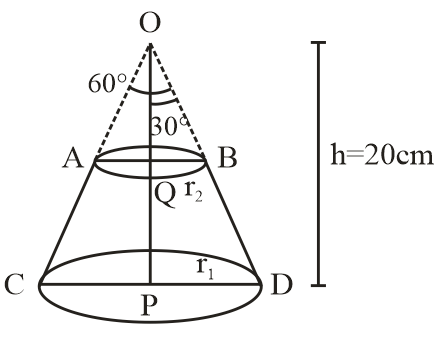
According to the question height h(OP) is divided in 2 equal parts.
So, OQ=OP=10cm
Here QP is also height of frustum
Let QB be the radius r2 of frustum and PD, radius r1 of frustum.
It is given that ∠AOB=60∘
So, ∠QOB=30∘
Now, we need to find r1 and r2.
In right ΔOPD
tanθ=OPPD
tanθ=20r1
tan30∘=20r1
r1=320cm …..(1)
In right triangle, ΔOQB
tanθ=OQQB
tan30∘=10r2
31=10r2 or r2=310cm …..(2)
Now, volume of frustum ABCD,
,
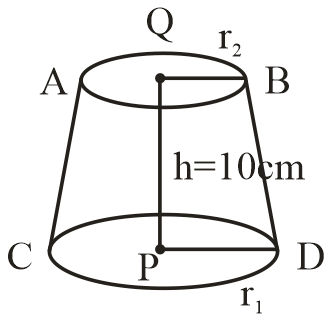
Vf=3πh(r12+r22+r1r2)
=3π×10[(320)2+(310)2+320+310]
Vf=3π10[3400+3100+3200]
Vf=3×310π(700)
Vf=9700πcm3 …..(3)
Now, volume of cylindrical were =πr2h
It is given that diameter of wire is 161cm
So, radius r=2d=16×21=321cm
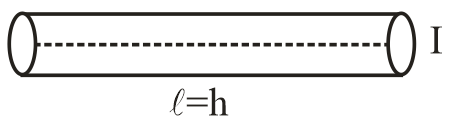
r=321cm
As length of wire is height of cylinder = h cm
Volume of wire =πr2h
Vw=π[321]2×h …..(4)
As wire is made of material used in frustum,
So volume of wire = volume of frustum
Therefore by equation 3 and 4
Vw=Vf
π×32×321×h=9700π
or, h=9700×32×32cm
h=97168000=796444.4cm
Therefore length of wire =796444.4cm
=7964.4m
Note : Here in calculation for radii r1 and r2 of frustum, we took two triangles.
Here is the explanation of finding tanθ.
Our diagram was
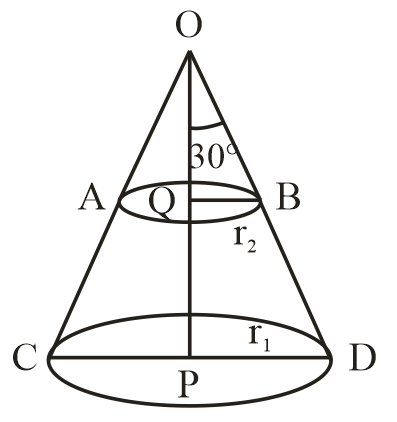
For ΔOQB
∠Q=90∘ and θ is given at ∠QOB. So side opposite to 90∘ i.e., OB = hypotenuse and side opposite to θ i.e., ∠QOB is QB will be the perpendicular of ΔOQB.
So, base =OQ=10cm,Hypotenuse = OB ; perpendicular =QB=
We know that tanθ=baseperpendicular
tanθ=10r2
θ=30∘
tan30∘=10r2
So, r2=310cm
Same goes for triangle OPD.
