Question

A metal wire of resistance $3\Omega$ is elongated to make a uniform wire of double its previous length. This new wire is now bent and the ends joined to make a circle. If two points on this circle. If two points on this circle makes an angle $60{}^\circ$ at the centre, the equivalent resistance between these two points will be?
$$$$ $\begin{aligned} & A)\dfrac{12}{5}\Omega \\\ & B)\dfrac{5}{3}\Omega \\\ & C)\dfrac{5}{2}\Omega \\\ & D)\dfrac{7}{2}\Omega \\\ \end{aligned}$

Answer 1

We can solve this problem by using the concept that the resistivity of a material is always constant. The term resistivity arises from the dependence of resistance on length and area of cross section. We must know that resistance is directly proportional to length and inversely proportional to area of cross section. While we elongate the wire, its volume also remains constant.

Formula used:

& R=\rho \dfrac{l}{A} \\\ & {{R}_{new}}={{n}^{2}}\times {{R}_{old}} \\\ \end{aligned}$$ **Complete step by step solution:** First of all I will explain how the relation $${{R}_{new}}={{n}^{2}}\times {{R}_{old}}$$ was derived. We know, resistivity of a material remains constant.so, while elongating the wire, there will be a change in resistance happening. We must keep in mind that the volume of the wire also remains constant. Let, 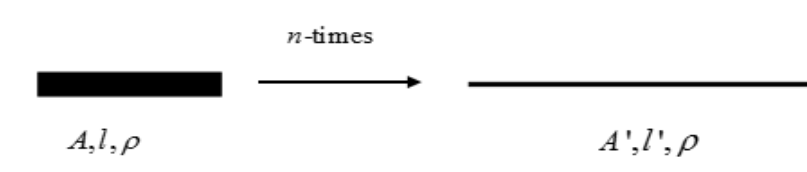 $$n$$ is the ratio between new length and old length. i.e. $$n=\dfrac{l'}{l}$$ By the concept, volumes remains same, $$\begin{aligned} & Al=A'l' \\\ & \Rightarrow \dfrac{l'}{l}=\dfrac{A}{A'}=n \\\ \end{aligned}$$ --- (1) From equation of resistivity, $${{R}_{old}}=\rho \dfrac{l}{A}$$ --- (2) $${{R}_{new}}=\rho \dfrac{l'}{A'}$$ --- (3) By dividing 3 by 2, $$\dfrac{{{R}_{new}}}{{{R}_{old}}}=\dfrac{\rho \dfrac{l'}{A'}}{\rho \dfrac{l}{A}}=\dfrac{l'}{l}\times \dfrac{A}{A'}$$ $$\Rightarrow \dfrac{{{R}_{new}}}{{{R}_{old}}}=n\times n={{n}^{2}}$$ -- (A/A’=n from (1)) That means, $${{R}_{new}}={{n}^{2}}\times {{R}_{old}}$$ Given in the question, $${{R}_{old}}=3\Omega $$ and $$l$$ is doubled, i.e.$$n=2$$ . $$\Rightarrow {{R}_{new}}={{2}^{2}}\times 3\Omega =4\times 3=12\Omega $$ . Therefore, the new resistance is $$12\Omega $$ . Now, this wire is bent to a circle and formed into a circle and 2 points make $$60{}^\circ $$ at the centre. If we draw this, it will be like, 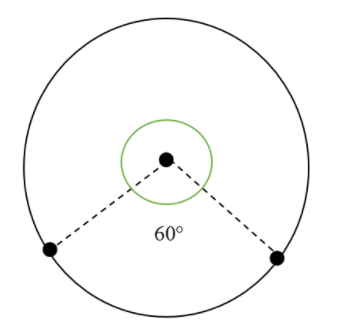 Now, from the figure, we can understand that the piece with $$300{}^\circ $$ angle will have a resistance of, $${{R}_{1}}=\dfrac{300{}^\circ }{360{}^\circ }\times 12\Omega =\dfrac{5}{6}\times 12=10\Omega $$ --- (obtained by taking proportion of the circumference) And resistance of the remaining part with $$60{}^\circ $$ angle is, $${{R}_{2}}=\dfrac{60{}^\circ }{360{}^\circ }\times 12\Omega =\dfrac{1}{6}\times 12=2\Omega $$ Now, we need to find the equivalent resistance between two points. If we examine the figure we can find that these two resistance are in parallel connection.so, equivalent resistance is given by, $${{R}_{equivalent}}=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}=\dfrac{10\times 2}{10+2}=\dfrac{20}{12}=\dfrac{5}{3}\Omega $$ **So, the correct answer is “Option B”.** **Note:** This question will be easier if we have idea about the equation, $$R=\dfrac{\rho {{l}^{2}}}{AlD}d=\dfrac{\rho {{l}^{2}}d}{m}$$ this equation is obtained by input of certain variables and converting the basic equation into this. From this we can easily find the new resistance as $${{R}_{new}}\propto {{l}^{2}}$$ and hence find the new resistance.