Question

A metal sphere with its centre at A and radius R has a charge 2q on it. The field at a point B outside the sphere is E. If another metal sphere of radius 3R and having a charge – 3q is placed with its centre at point B, the resultant electric field at a point midway between A and B will be:
A) $0.5E$
B) $2E$
C) $2.5E$
D) $10E$

Answer 1

At a point in the middle of the two charged objects, there are two electric fields acting on it. The resultant electric field can be expressed in terms of the given electric field E, here, to obtain the answer.
Another theory used in this problem is that a sphere containing charge on its surface behaves like a point charge.

Complete step by step answer:
In this problem, there are two metal spheres of radii R and 3R respectively with their centres at A and B respectively.
The electric field is defined as the force applied on an unit positive charge when it is placed at a distance r from a point charge.
The mathematical expression is given by –
$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}}$
The electric field at any point outside the sphere with charge q, at a distance of r from the centre of the sphere, is given by the formula –
$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}}$
where ${\varepsilon _0}$= permittivity of free space.
This formula is similar to that of a point charge.
Hence, it can be said that a metal sphere containing the charge behaves like a point charge.
Therefore, in this problem, the radii R and 3R can be ignored since, the two metal spheres are reduced to point charges at A and B as shown:

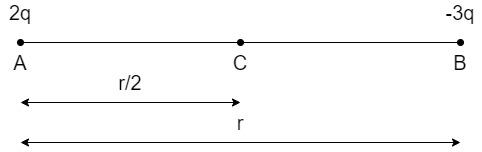
Let r be the distance of separation from A and B and C be the midpoint of the line joining A and B as shown in the above figure.
The electric field acting on B due to A is given as E.
The electric field acting at point C due to the charges A and B is given as –

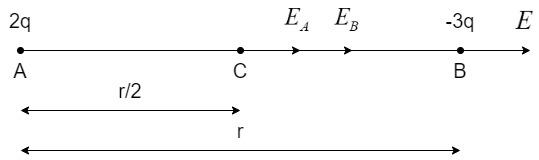
The electric field acting on B due to A, E is represented as –
$\Rightarrow E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{{{r^2}}}$
The electric field acting on C due to A, is
$\Rightarrow {E_A} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{{{r^2}}} \times 4$
Substituting the value of E in the above equation,
$\Rightarrow {E_A} = 4E$
Similarly, the electric field on C due to B –
$\Rightarrow {E_B} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - 3q}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{12q}}{{{r^2}}}$
$\Rightarrow {E_B} = 6 \times \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{{{r^2}}} = 6E$
From the above figure, the net electric field at C,
$\Rightarrow {E_{net}} = {E_A} - {E_B}$
$\Rightarrow {E_{net}} = 4E + 6E = 10E$

Therefore, the net electric field at the mid-way of A and B = 10E.

Note: For a positive charge, the electric field will be oriented in the outward direction away from the charge. For a negative charge, the electric field will be oriented in the inward direction towards the charge. This is why the direction of the electric field due to B on C is written negative.