Question

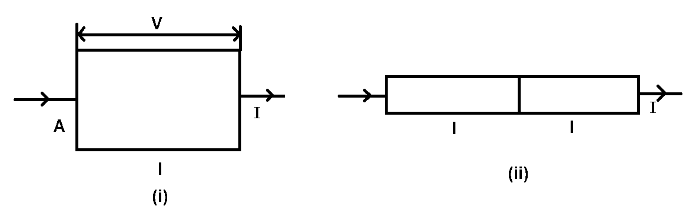
A metal rod of square cross-sectional area $A$ having length $l$ has current $I$ flowing through it when a potential difference of $V$ volt is applied across its ends (figure ii). What potential difference must be maintained across the length $2l$ so that the current in the rod is still $I$?

Answer 1

From the figure, we can say that the rod in figure i is cut parallel and is rejoined by length as shown in figure ii making its length change. Due to this, its cross sectional area is changed and these both in turn will affect the value of resistance. After getting the value for this new resistance, we will apply Ohm’s law to find the required potential difference.

Formulas used:
$V = IR$,
where, $V$ is the potential difference, $I$ is the current and $R$ is the resistance.
$R = \dfrac{{\rho l}}{A}$ ,
where, $R$ is the resistance, $\rho$ is the resistivity of the material, $l$ is the length and $A$ is the cross-sectional area.

Complete step by step answer:
Let us first consider figure I where a metal rod of square cross-sectional area $A$having length $l$ has current $I$ flowing through it when a potential difference of $V$volt is applied across its ends. If we take resistance in this case as $R$and apply the Ohm’s law, we get
$V = IR$
And $R = \dfrac{{\rho l}}{A}$

Now, in the second case, the metal rod is cut parallel and is rejoined by length as shown in figure ii making its length double which is $2l$. Due to this, its cross-sectional area becomes half which is $\dfrac{A}{2}$. Therefore, new resistance for this case is
$R' = \dfrac{{\rho \left( {2l} \right)}}{{\left( {\dfrac{A}{2}} \right)}}\\\ \Rightarrow R' = 4\dfrac{{\rho l}}{A} \\\ \Rightarrow R' = 4R$
It is given that the current should remain the same as the previous case which is $I$.
Therefore, when we apply Ohm’s law, we get
${V^1} = I R' \\\ \Rightarrow{V^1} = I\left( {4R} \right) \\\ \Rightarrow{V^1} = 4IR \\\ \therefore{V^1} = 4V$

Thus, the potential difference must be maintained across the length $2l$ so that the current in the rod is still $I$ is four times the original voltage.

Note: In this problem, we have seen that the potential difference is dependent on resistance when the current is constant. Also, in this case the rod is cut parallel which doubles its length and decreases its cross-sectional area to half of its original value. Both these parameters affect the resistance and therefore in any case, if it is given that length or area is changing, then we can find the corresponding value of resistance and then apply the Ohm’s law to find the required potential difference.