Question
Question: A metal rod of length $\ell$, radius $r$ and mass $m$ rests at the one end of a parallel conducting ...
A metal rod of length ℓ, radius r and mass m rests at the one end of a parallel conducting rail of length L, carrying constant current I as shown. Now a uniform magnetic field of magnitude B switched on normal to the plane of rail. The translational kinetic energy of rod when it reaches the other end without slipping is
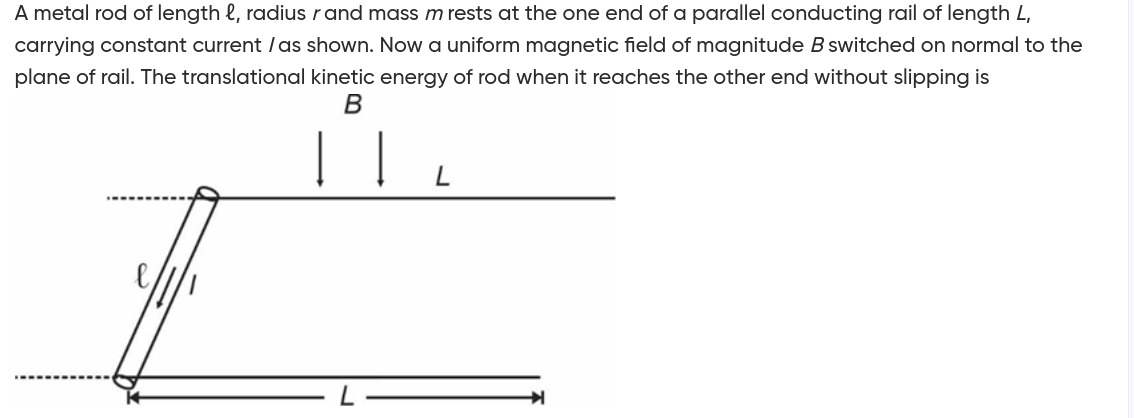
21IℓBL
32IℓBL
43IℓBL
IℓBL
32IℓBL
Solution
The magnetic force on the rod is given by F=IℓB. The work done by this force over the distance L is W=F⋅L=IℓBL. Since the rod rolls without slipping, its total kinetic energy is the sum of its translational and rotational kinetic energies: KE=21mv2+21Iω2. For a cylinder rolling without slipping, I=21mr2 and ω=rv. Thus, KE=21mv2+21(21mr2)(rv)2=43mv2. By the work-energy theorem, W=KE, so IℓBL=43mv2. The translational kinetic energy is 21mv2=32IℓBL.
