Question

The rod is vibrating in a frequency higher than that in fundamental. Which frequency is the first higher frequency (in kHz) above fundamental mode for all the parts to resonate ?

• A. 40
• B. 80
• C. 120
• D. 160

Answer 1

Answer: (C)

120

Answer 2

The speed of longitudinal waves in the rod is given by $v = \sqrt{\frac{Y}{\rho}}$. Given $Y = 1.6 \times 10^{11}$ N/m² and $\rho = 2500$ kg/m³.

$v = \sqrt{\frac{1.6 \times 10^{11}}{2500}} = \sqrt{64 \times 10^6} = 8000$ m/s.

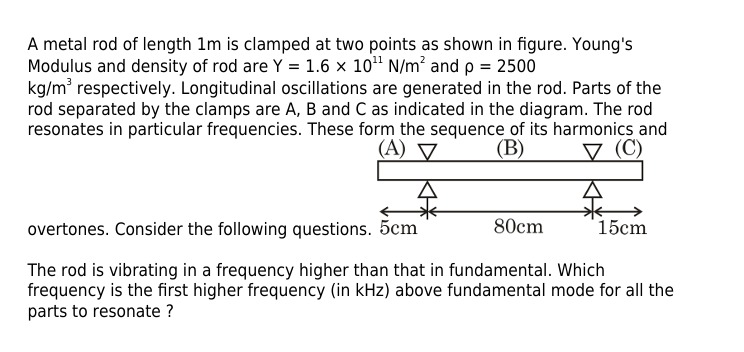
The rod is clamped at 5 cm and 85 cm from one end, dividing it into three parts:

• Part A: Length $L_A = 5$ cm = 0.05 m. Free at one end, clamped at the other.
• Part B: Length $L_B = 85 - 5 = 80$ cm = 0.80 m. Clamped at both ends.
• Part C: Length $L_C = 100 - 85 = 15$ cm = 0.15 m. Clamped at one end, free at the other.

For longitudinal oscillations, the clamped ends are displacement nodes, and the free ends are displacement antinodes.

The allowed frequencies for each part are:

• Part A (Free-Clamped): $f_A = (2n_A - 1)\frac{v}{4L_A}$, where $n_A = 1, 2, 3, ...$

  $f_A = (2n_A - 1)\frac{8000}{4 \times 0.05} = (2n_A - 1)\frac{8000}{0.2} = (2n_A - 1) \times 40000$ Hz $= (2n_A - 1) \times 40$ kHz.

  Possible frequencies for A: $\{40, 120, 200, 280, 360, 440, 520, 600, ...\}$ kHz.

• Part B (Clamped-Clamped): $f_B = n_B\frac{v}{2L_B}$, where $n_B = 1, 2, 3, ...$

  $f_B = n_B\frac{8000}{2 \times 0.80} = n_B\frac{8000}{1.6} = n_B \times 5000$ Hz $= n_B \times 5$ kHz.

  Possible frequencies for B: $\{5, 10, 15, 20, ..., 40, ..., 120, ..., 200, ..., 600, ...\}$ kHz.

• Part C (Clamped-Free): $f_C = (2n_C - 1)\frac{v}{4L_C}$, where $n_C = 1, 2, 3, ...$

  $f_C = (2n_C - 1)\frac{8000}{4 \times 0.15} = (2n_C - 1)\frac{8000}{0.6} = (2n_C - 1) \times \frac{40000}{3}$ Hz $= (2n_C - 1) \times \frac{40}{3}$ kHz.

  Possible frequencies for C: $\{\frac{40}{3}, 40, \frac{200}{3}, \frac{280}{3}, 120, \frac{440}{3}, \frac{520}{3}, 200, ...\}$ kHz.

For all parts to resonate at the same frequency $f$, the frequency must be common to all three sets.

$f = (2n_A - 1) \times 40 = n_B \times 5 = (2n_C - 1) \times \frac{40}{3}$.

From $(2n_A - 1) \times 40 = n_B \times 5$, we get $8(2n_A - 1) = n_B$. Since $n_A \ge 1$, $2n_A - 1$ is an odd integer $\ge 1$. So $n_B$ must be a multiple of 8. The common frequencies for A and B are the odd multiples of 40 kHz.

From $(2n_A - 1) \times 40 = (2n_C - 1) \times \frac{40}{3}$, we get $3(2n_A - 1) = (2n_C - 1)$. Let $k_A = 2n_A - 1$ and $k_C = 2n_C - 1$. Both $k_A$ and $k_C$ are odd integers $\ge 1$. We have $3k_A = k_C$.

Since $k_A$ is an odd integer ($1, 3, 5, ...$), $k_C$ must be an odd integer that is a multiple of 3 ($3, 9, 15, ...$). This is consistent with $k_C$ being an odd integer.

The common frequencies for A and C are $f = 40 k_A$, where $k_A$ is an odd integer. These are $\{40, 120, 200, 280, ...\}$ kHz.

We need frequencies common to A, B, and C. These frequencies must be in the set $\{40, 120, 200, 280, ...\}$ kHz, and also be multiples of 5 kHz (from part B). Since all numbers in the set $\{40, 120, 200, 280, ...\}$ are multiples of 40, they are also multiples of 5.

So, the common resonant frequencies for all three parts are $\{40, 120, 200, 280, 360, 440, 520, 600, ...\}$ kHz.

The fundamental frequency for all parts to resonate is the lowest frequency in this set, which is 40 kHz.

The question asks for the first higher frequency above the fundamental mode for all parts to resonate. This is the next frequency in the common set, which is 120 kHz.

At 40 kHz:

$f = 40 = (2n_A - 1) \times 40 \implies 2n_A - 1 = 1 \implies n_A = 1$ (fundamental for A)

$f = 40 = n_B \times 5 \implies n_B = 8$ (8th harmonic for B)

$f = 40 = (2n_C - 1) \times \frac{40}{3} \implies 3 = 2n_C - 1 \implies 2n_C = 4 \implies n_C = 2$ (first overtone for C, since $n_C=1$ is fundamental)

At 120 kHz:

$f = 120 = (2n_A - 1) \times 40 \implies 2n_A - 1 = 3 \implies n_A = 2$ (first overtone for A)

$f = 120 = n_B \times 5 \implies n_B = 24$ (24th harmonic for B)

$f = 120 = (2n_C - 1) \times \frac{40}{3} \implies 120 \times \frac{3}{40} = 2n_C - 1 \implies 9 = 2n_C - 1 \implies 2n_C = 10 \implies n_C = 5$ (fourth overtone for C)

The fundamental frequency for all parts to resonate is 40 kHz. The first higher frequency for all parts to resonate is 120 kHz.