Question

A metal rod of length 1 m is clamped at two points as shown in the figure. Distance of the lamps from two ends are 5 cm and 15 cm respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young’s modulus of elasticity and density of aluminium are $Y=1.6\times {{10}^{11}}N{{m}^{-2}}$ and $\rho =2500kg{{m}^{-3}}$ respectively.

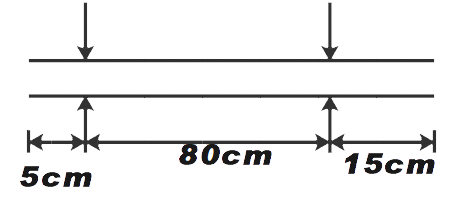
A. 40 kHz, 120 kHz
B. 120 kHz, 40 kHz
C. 40 kHz, 40 kHz
D. 1200 kHz, 120 kHz

Answer 1

To solve this question, we will first calculate the speed of the longitudinal wave. We know that in a wave a node is formed and in between the nodes the integer number loops will be formed. Therefore, we will calculate the number of loops formed. We will then calculate the wavelength of the wave. Later, we will calculate the minimum frequency using these values. And similarly, we will calculate the next higher frequency of natural longitudinal oscillation of the rod.

Formula used:
$v=\sqrt{\dfrac{Y}{\rho }}$
Where,
V is the velocity of the longitudinal wave
${{f}_{\min }}=\dfrac{v}{\lambda }$
Where,
$\lambda$ is the wavelength

Complete step-by-step answer:
To calculate the frequency, we first need to know the speed of the wave.
We know that,
The speed of the longitudinal wave is given by,
$v=\sqrt{\dfrac{Y}{\rho }}$
After substituting the given values,
We get,
$v=\sqrt{\dfrac{1.6\times {{10}^{11}}}{2500}}$
Therefore,
$v=8000m/ s$
Now, we know that nodes are formed where the rod is clamped. Therefore, the number of integer loops in between the node where rod is clamped i.e. between QR will be given by,
${{n}_{1}}\dfrac{\lambda }{2}=80$
Therefore,
${{n}_{1}}\lambda =160$ …………………….. (1)
Similarly, between PQ, Q is fixed end and P is the free end
Therefore, we know that loops formed between PQ will be odd multiple of $\dfrac{\lambda }{4}$
Therefore,
$\dfrac{(2{{n}_{2}}-1)\lambda }{4}=5$ ……………… (A)
$(2{{n}_{2}}-1)\lambda =20$…………… (2)
Similarly, we can say for RS the number of loops will be given by,
$\dfrac{(2{{n}_{3}}-1)\lambda }{4}=15$
$(2{{n}_{3}}-1)\lambda =60$ ………………….. (3)
Now, from (1) and (2)
We can say that,
$\dfrac{{{n}_{1}}}{2{{n}_{2}}-1}=\dfrac{160}{20}=8$ ……………………… (4)
Similarly, from (1) and (3)
$\dfrac{{{n}_{1}}}{2{{n}_{3}}-1}=\dfrac{160}{60}=\dfrac{8}{3}$ …………………….. (5)
We know, for minimum frequency the number of loops should be minimum
Therefore, from (4) and (5)
We can say that,
${{n}_{1}}=8,{{n}_{2}}=1,{{n}_{3}}=2$
Substituting the value of ${{n}_{2}}$ in equation (A)
We get,
$\lambda =\dfrac{20}{2{{n}_{2}}-1}$
Therefore,
$\lambda =20cm=0.2m$
Now we know that minimum frequency is given by,
${{f}_{\min }}=\dfrac{v}{\lambda }$
After substituting the values,
We get,
${{f}_{\min }}=\dfrac{800}{0.2}$
${{f}_{\min }}=40000Hz$
This can also be written as,
${{f}_{\min }}=40$kHz
Now, we know that next higher frequency will correspond to $\dfrac{3\lambda }{4}$for PQ
Therefore, by doing similar calculations
We get,
$f'=120$kHz

So, the correct answer is “Option A”.

Note: We know that in a rod longitudinal waves travel along the length. These waves interfere with each other constructively or destructively. When the waves cancel each other out the point is called the node and when the waves add up to form a bigger wave also known as constructive interference of the wave, such points are the antinodes. The waves vibrate in antinodes. So, when the rod is clamped at point the nodes are formed.