Question

A metal rod AB of length $10x$ has its one end A in ice at $0{}^\circ C$ and the other end B in water at $100{}^\circ C$. If a point P on the rod is maintained at $400{}^\circ C$, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540cal/g and latent heat of melting of ice is 80cal/g. If the point P is at a distance of $\lambda x$ from the ice end A, find the value of λ. (Neglect any heat loss to the surrounding).

Answer 1

We are given the length and the temperatures at the two ends of a metal rod. It is said that there is a point on the rod where the temperature is higher than the temperature at the ends. It is also said that equal amounts of water and ice evaporate and melt per unit time. Therefore we can find the rate of melting of ice and rate of evaporation of water using the given data and equate them. Thus we will get the required solution.
Formula used:
$\dfrac{dQ}{dt}=\dfrac{KA\Delta T}{d}$

Complete answer:
In the question we are given a metal rod with its one end at ice and the other end in water.
The temperature of the end A is $0{}^\circ C$ and the end B is $100{}^\circ C$.
It is said there is a point P on the rod and the temperature at point P is maintained at $400{}^\circ C$.
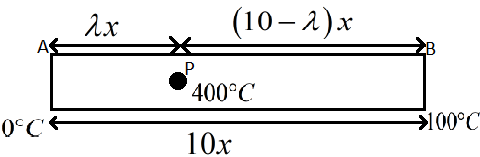
The total length of the rod AB is given as $10x$ and the distance from A to P is given as $\lambda x$.
Therefore we know that the distance from P to the end B will be,
$\begin{aligned} & 10x-\lambda x \\\ & \Rightarrow \left( 10-\lambda \right)x \\\ \end{aligned}$
The figure below shows the given situation.

We know that the heat will flow from higher temperature to lower temperature.
Therefore in this case the heat will flow from point P to A and from point P to B.
Let ‘${{Q}_{1}}$ be the heat change from P to A.
Then,
${{Q}_{1}}=\dfrac{d{{m}_{i}}}{dt}=\dfrac{KA\Delta T}{\left( \lambda x \right){{L}_{i}}}$, were ‘$\left( \dfrac{d{{m}_{i}}}{dt} \right)$’ is the rate of melting of ice per unit time, ‘K’ is the thermal conductivity of the rod, ‘A’ is the area, ‘$\Delta T$’ is the temperature difference between ‘P’ and ‘A’, ‘$\lambda x$’ is the distance between ‘P’ and ‘A’ and ‘${{L}_{i}}$’ is the latent heat of melting of ice.
We are given, ${{L}_{i}}=80cal/g$.
We know that the temperature difference, $\Delta T=400{}^\circ C-0{}^\circ C=400{}^\circ C$
Therefore we get,
$\Rightarrow {{Q}_{1}}=\dfrac{d{{m}_{i}}}{dt}=\dfrac{KA\times 400}{\left( \lambda x \right)80}$
Let ‘${{Q}_{2}}$’ be the heat change from P to A. then,
${{Q}_{2}}=\dfrac{d{{m}_{w}}}{dt}=\dfrac{KA\Delta T}{\left( 10-\lambda \right)x\left( {{L}_{w}} \right)}$, were ‘$\left( \dfrac{d{{m}_{w}}}{dt} \right)$’ is the rate of evaporation of water per unit time.
We are given latent heat of vaporization of water, ${{L}_{w}}=540cal/g$
We know that the temperature difference, $\Delta T=400{}^\circ C-100{}^\circ C=300{}^\circ C$
Therefore,
$\Rightarrow {{Q}_{2}}=\dfrac{d{{m}_{w}}}{dt}=\dfrac{KA\times 300}{\left( 10-\lambda \right)x\times \left( 540 \right)}$
In the question it is also said that the rate of evaporation of water per unit time is equal to the rate of melting of ice per unit time, i.e.
$\dfrac{d{{m}_{i}}}{dt}=\dfrac{d{{m}_{w}}}{dt}$
Therefore, by equating this we get
$\Rightarrow \dfrac{KA\times 400}{\left( \lambda x \right)80}=\dfrac{KA\times 300}{\left( 10-\lambda \right)x\times \left( 540 \right)}$
By eliminating the common terms we get,
$\Rightarrow \dfrac{400}{80\lambda }=\dfrac{300}{\left( 10-\lambda \right)540}$
$\Rightarrow \dfrac{5}{\lambda }=\dfrac{5}{\left( 10-\lambda \right)9}$
$\Rightarrow \dfrac{1}{\lambda }=\dfrac{1}{90-9\lambda }$
$\Rightarrow 90-9\lambda =\lambda$
$\Rightarrow 10\lambda =90$
$\Rightarrow \lambda =\dfrac{90}{10}=9$
Hence the value of $\lambda$ is 9.

Note:
The movement of heat in a system due to difference in temperature within the system or between the system and surrounding is known as heat transfer. This difference in temperature that causes the flow of heat is known as potential.
There are several ways of heat transfer like conduction, convection and radiation.
In the process of conduction the heat flows from the system with higher temperature to the lower temperature.
During convection the fluid particles move from higher temperature to lower temperature.
In radiation heat is transferred without any physical contact through electromagnetic waves.