Question

A metal ring of radius $r = 0 \cdot 5m$ with its plane normal to a uniform magnetic field B of induction $0 \cdot 2T$ carries a current$I = 100A$. The tension in newtons developed in the ring is:
A) 100
B) 50
C) 25
D) 10

Answer 1

If a current carrying coil is placed under the presence of the magnetic field then the coil experiences a force. The direction of magnetic field developed by the current carrying coil can be found by using right hand thumb rule.

Formula used: The formula of the force experienced by the coil carrying current is given by,
$F = I \cdot B \cdot L$
Where I is the current B is the magnetic force and L is the length of the coil.

Complete step-by-step answer:
It is given in the problem that a metal ring of $r = 0 \cdot 5m$ with its plane to a magnetic field B of induction $0 \cdot 2T$ which carries a current $I = 100A$ and we need to find the tension that develops in the ring.

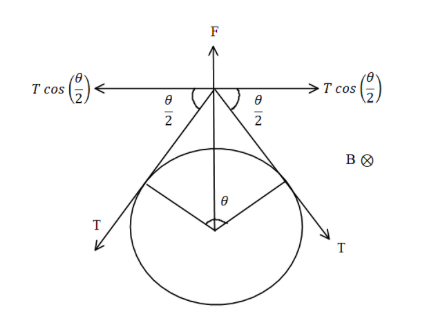
The tension developed in the x-direction gets cancelled out but the tension developed in the y-direction can be solved further.
$\Rightarrow {F_T} = 2T\dfrac{{\sin \theta }}{2}$
As the angle $\theta$ is very small therefore$\sin \theta \approx \theta$.
$\Rightarrow {F_T} = 2T\left( {\dfrac{{\sin \theta }}{2}} \right)$
$\Rightarrow {F_T} = 2T\left( {\dfrac{\theta }{2}} \right)$………eq. (1)
The formula of the force experienced by the coil carrying current is given by,
$F = I \cdot B \cdot L$
Where I is the current B is the magnetic force and L is the length of the coil.
The force on the coil for the small element $\Delta L$ is given by,
$\Rightarrow F = I \cdot B \cdot \Delta L$………eq. (2)
Equating force from equation (1) and equation (2).
$\Rightarrow I \cdot B \cdot \Delta L = 2T\left( {\dfrac{\theta }{2}} \right)$
$\Rightarrow I \cdot B \cdot \Delta L = 2T\left( {\dfrac{\theta }{2}} \right)$
$\Rightarrow I \cdot B \cdot \Delta L = T \cdot \theta$
$\Rightarrow I \cdot B \cdot \Delta L = 2T \cdot \theta$………eq. (3)
As the length of the arc of the circle is given by,
$\Delta L = r \cdot \theta$
Using $\Delta L = r \cdot \theta$ equation in (3)
$\Rightarrow I \cdot B \cdot \Delta L = T \cdot \theta$
$\Rightarrow I \cdot B \cdot \left( {r \cdot \theta } \right) = T \cdot \theta$
$\Rightarrow T = I \cdot B \cdot r$
Replace the value of the current, magnetic field and radius of the coil in the above relation.
$\Rightarrow T = I \cdot B \cdot r$
$\Rightarrow T = \left( {100} \right) \times \left( {0 \cdot 2} \right) \times \left( {0 \cdot 5} \right)$
$\Rightarrow T = 10N$.
The tension in the ring will be equal to $T = 10N$.

The correct answer for this problem is option D.

Note: The current carrying coil generates its own magnetic field and when this current carrying coil is placed in an external magnetic field then there can be attraction or repulsion between the magnetic field of the coil and external magnetic field. The attraction and repulsion between the coil and the external magnetic field depends on the nature of the magnetic fields.