Question

A metal ring of mass m and radius r is placed on a smooth horizontal table and is set rotating about its axis so that each part of the ring moves with a speed, v. The tension in the ring is –
A. $\dfrac{{m{v^2}}}{{2\pi r}}$
B. $\dfrac{{m{v^2}}}{r}$
C. $\dfrac{{m{v^2}}}{{\pi {r^2}}}$
D. $\dfrac{{m{v^2}}}{{2r}}$

Answer 1

When a body is moving about its axis, there is a force acting on it which pulls the object towards the center. This force is called the centripetal force. The expression for centripetal force is given by –
$F = \dfrac{{m{v^2}}}{r}$

Complete step by step solution:
Consider a small line element of the ring $dx$ with included angle $\theta$ as shown:

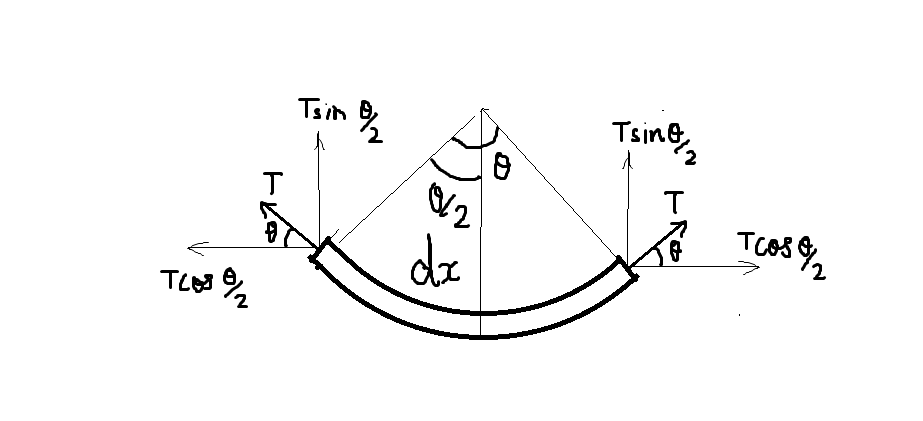
If M is the mass of the ring and R is the radius of the ring, then
The mass per unit length of the ring –
$m = \dfrac{M}{{2\pi R}}$
Thus, the mass of the line element $dx$ –
$dm = \dfrac{{M.dx}}{{2\pi R}}$
Since the ring is rotating, there is a centripetal force acting on the ring element. This centripetal force is equal to the tension on either side of the ring.
However, we see in the diagram that tension is acting along with the ring element. Thus, we must resolve the tension force into its components – $T\sin \dfrac{\theta }{2}$ and $T\cos \dfrac{\theta }{2}$
Now, the 2 components of $T\cos \dfrac{\theta }{2}$cancel out each other and the other component $T\sin \dfrac{\theta }{2}$acts on the ring. This is equal to the centripetal force.
$2T\sin \dfrac{\theta }{2} = \dfrac{{m{v^2}}}{R} \\\ 2T\sin \dfrac{\theta }{2} = \dfrac{{dm.{v^2}}}{R} \\\$
Substituting the value of $dm$ -
$2T\sin \dfrac{\theta }{2} = \dfrac{{M.dx}}{{2\pi R}} \times \dfrac{{{v^2}}}{R}$
Since $\theta$ is very small, $\sin \theta \approx \theta$
$2T\dfrac{\theta }{2} = \dfrac{{M.dx}}{{2\pi R}} \times \dfrac{{{v^2}}}{R} \\\ T\theta = \dfrac{{M.dx}}{{2\pi R}} \times \dfrac{{{v^2}}}{R} \\\$
The angle $\theta = \dfrac{{dx}}{R}$
$T\left( {\dfrac{{dx}}{R}} \right) = \dfrac{{M.dx}}{{2\pi R}} \times \dfrac{{{v^2}}}{R}$
This is a differential equation. Solving the above differential equation w.r.t dx

$$\int {T\left( {\dfrac{{dx}}{R}} \right)} = \int {\dfrac{{M.dx}}{{2\pi R}} \times \dfrac{{{v^2}}}{R}} \\\ \dfrac{T}{R}\int {dx = \dfrac{{M{v^2}}}{{2\pi {R^2}}}} \int {dx} \\\ \int {dx = 1} \\\ \therefore \\\ \dfrac{T}{{{R}}} = \dfrac{{M{v^2}}}{{2\pi {R^{{2}}}}} \\\ T = \dfrac{{M{v^2}}}{{2\pi R}} \\\$$

$\therefore$ Hence, the correct answer is Option A.

Note:
Students generally, confused while writing the horizontal and vertical components of a vector. You can use a simple and handy thumb rule as shown here:

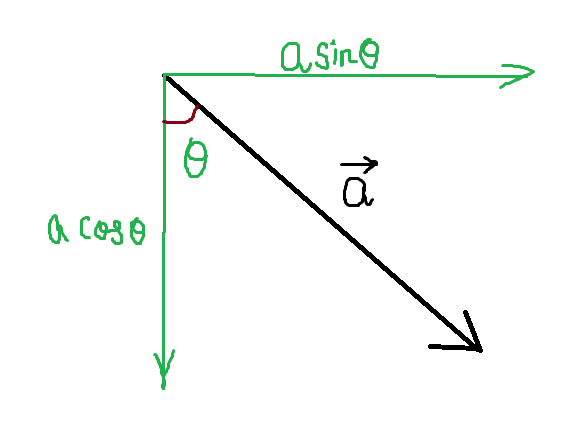
Consider a vector $\vec a$ inclined at angle $\theta$ as shown in the above figure:
- The line that is attached to the angle $\theta$ is designated as $\cos \theta$.
- The other line that is not attached to the angle$\theta$ is designated as $\sin \theta$.