Question

A metal plate of area $A = 0.01{m^2}$carries a charge of $100uC$. Calculate the outward pull on one side of the plate. (k=1)

Answer 1

Consider a small area on the metal plate. Then, calculate the net electric field acting on the small area due to charges on the two surfaces of thin metal plates. Then, integrate over the entire area to find the net outward force on one side of the plate.

Formula used:
Force acting on charge $dq$ is given by $dF = E.dq$ …… (A)
Where $dF$ is the force due to field, $E$ is the net field at the position of $dq$ and $dq$ is test charge element.
Surface charge density: $\sigma = \dfrac{{{Q_{total}}}}{A}$ …… (B)
Where, $\sigma$ is surface charge density,${Q_{total}}$is total charge on surface$A$is total surface area.
Electric field outside metal plate of charge density $\sigma$ and Area $A$ given by: $E = \dfrac{\sigma }{\varepsilon }$ ….. (C)
Where $\varepsilon$ is the permittivity of space.
Electric field outside due to one surface of metal plate of charge density $\sigma$ and Area $A$ given by: $E = \dfrac{\sigma }{{2\varepsilon }}$ …… (D)
Where $\varepsilon$ is the permittivity of space.
The electric field inside any conductor E=0 …..(E)

Complete step by step answer:
Given,
${Q_{total}} = 100uC \Rightarrow {Q_{total}} = {10^{ - 4}}C$ as $1uC = {10^{ - 6}}C$
$A = 0.01{m^2}$
Let ${E_1}$ and ${E_2}$ be electric fields due to surface 1 and 2 respectively.

Step 1:
Using equation (B) we can find from given values,
$\sigma = \dfrac{{{{10}^{ - 4}}}}{{0.01}}C.{m^{ - 2}} = {10^{ - 2}}C.{m^{ - 2}}$ …… (1)

Step 2:
In figure gives an idea about the calculations below,

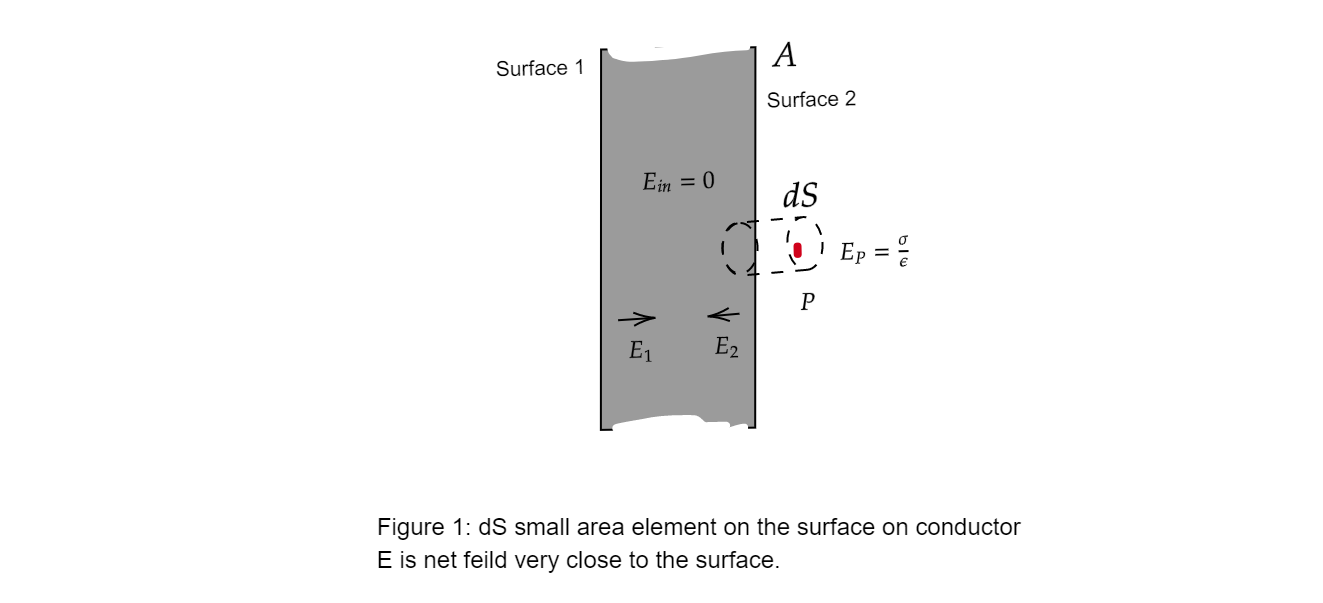
Electric field due to plate just outside at P: ${E_{plate}} = \dfrac{\sigma }{\varepsilon }$ …… (2)
The electric field just inside the plate region from equation (E) is 0.
${E_1} + {E_2} = {E_{inside}} = 0$
$\Rightarrow {E_1} + {E_2} = 0 \Rightarrow {E_1} = - {E_2}$ …… (3)
(negative sign says both are in opposite direction but equal in magnitude)

Step 3:
Putting values from equation (2) and (3) in equation (A) we get force,
$dF = {E_{net}}.dq$
$\Rightarrow dF = ({E_{plate}} - {E_1}).dq$
$\Rightarrow dF = (\dfrac{\sigma }{\varepsilon } - \dfrac{\sigma }{{2\varepsilon }}).dq = \dfrac{\sigma }{{2\varepsilon }}.dq$ …… (4) (outward)

Step 4:
We know, $dq = \sigma .dS$ …… (5)
Therefore, replacing equation (5) in equation (4) and integrating both sides we get,
$\Rightarrow \int_0^F {dF} = \int_0^A {\dfrac{\sigma }{{2\varepsilon }}.\sigma dS}$
$F = \dfrac{{{\sigma ^2}}}{{2\varepsilon }}\int_0^A {dS} = \dfrac{{{\sigma ^2}}}{{2\varepsilon }}A$ …… (6)
(since $\sigma$ and $\varepsilon$ are constant with respect to integral variable dS)

Step 5:
Replace the value of variables in equation 6 we get force acting on it outward
$F = \dfrac{{{\sigma ^2}}}{{2\varepsilon }}A$
$\Rightarrow F = \dfrac{{{{({{10}^{ - 2}})}^2}}}{{2 \times 8.854 \times {{10}^{ - 12}}}} \times {10^{ - 2}}N$
$\Rightarrow F = 0.05647 \times {10^6}N$
$\Rightarrow F = 56470N$

Net outward force =$F = 56470N$

Note:
Here, one should take care that just outside the metal surface, for point P metal plate appears infinitely big, therefore, we can use fields produced due to infinite metal plate carrying charge approximation.