Question

A metal piece of mass 160 g lies in equilibrium inside a glass of water (figure 13-E4). The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg m$^{-3}$, find the normal force exerted by the bottom of the glass on the metal piece.

Answer 1

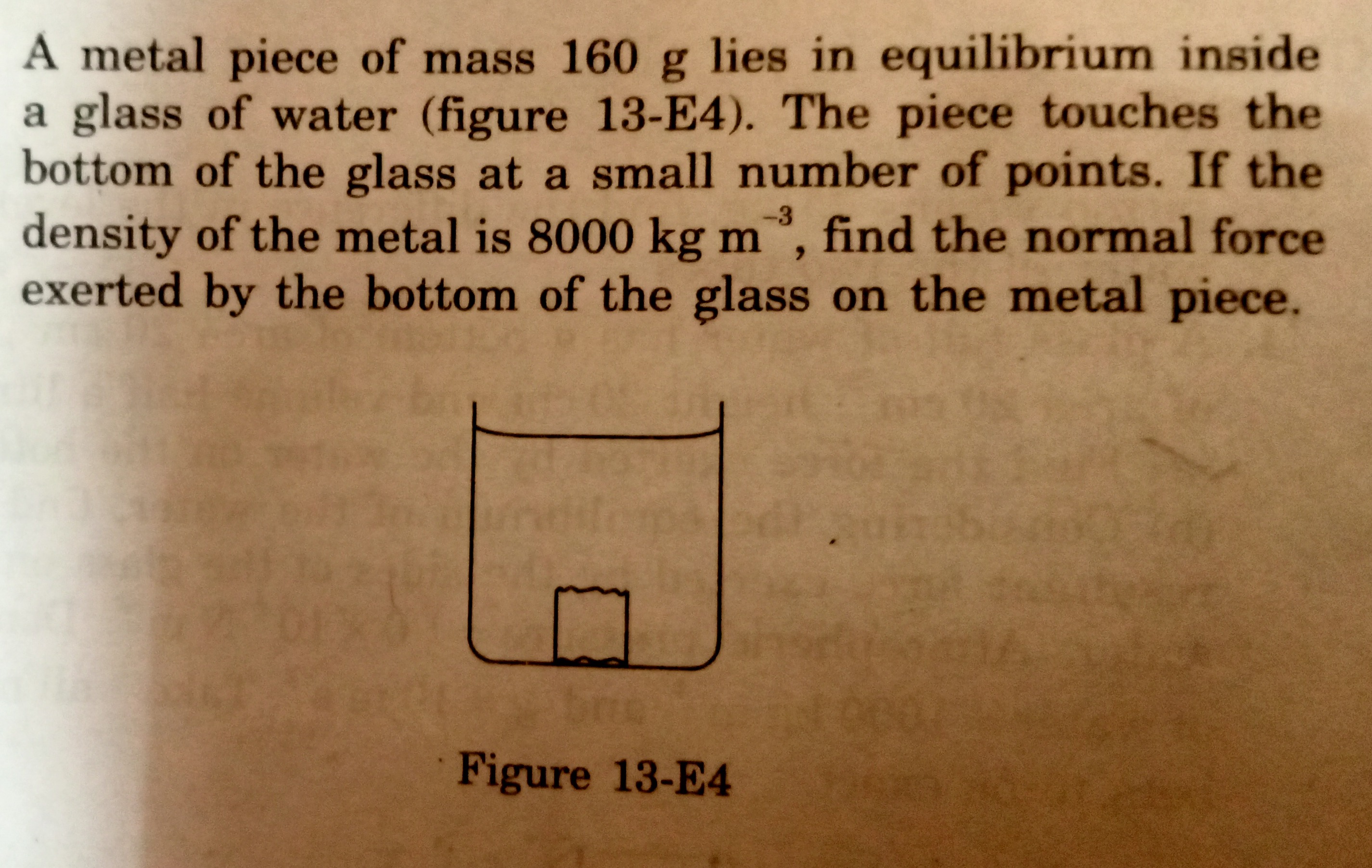
1.4 N

Answer 2

The metal piece is in equilibrium under the action of three forces:

1. Weight ($W$) acting downwards.
2. Buoyant force ($F_B$) acting upwards.
3. Normal force ($N$) exerted by the bottom of the glass acting upwards.

From the equilibrium condition, the sum of upward forces equals the downward force: $N + F_B = W$ Therefore, $N = W - F_B$.

1. Calculate the weight ($W$): Mass of the metal piece, $m = 160$ g $= 160 \times 10^{-3}$ kg. Assuming acceleration due to gravity $g = 10$ m/s$^2$. $W = mg = (160 \times 10^{-3} \text{ kg}) \times (10 \text{ m/s}^2) = 1.6$ N.

2. Calculate the volume of the metal piece ($V$): Density of the metal, $\rho_{metal} = 8000$ kg/m$^3$. $V = \frac{m}{\rho_{metal}} = \frac{160 \times 10^{-3} \text{ kg}}{8000 \text{ kg/m}^3} = \frac{0.16}{8000} \text{ m}^3 = 2 \times 10^{-5}$ m$^3$.

3. Determine the submerged volume and calculate the buoyant force ($F_B$): Density of water, $\rho_{water} = 1000$ kg/m$^3$. Since $\rho_{metal} > \rho_{water}$ (8000 kg/m$^3$ > 1000 kg/m$^3$), the metal piece sinks and is fully submerged. So, the submerged volume $V_{submerged} = V = 2 \times 10^{-5}$ m$^3$. The buoyant force is given by Archimedes' principle: $F_B = \rho_{water} \cdot V_{submerged} \cdot g$ $F_B = (1000 \text{ kg/m}^3) \times (2 \times 10^{-5} \text{ m}^3) \times (10 \text{ m/s}^2) = 0.2$ N.

4. Calculate the normal force ($N$): $N = W - F_B = 1.6 \text{ N} - 0.2 \text{ N} = 1.4$ N.