Question
Question: A metal block is heated well above the room temperature and then left to cool in the room. Choose th...
A metal block is heated well above the room temperature and then left to cool in the room. Choose the correct graph which shows the rate of cooling.
a. 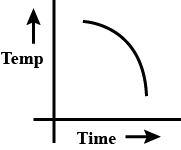
b. 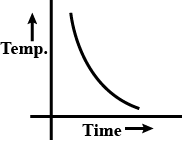
c. 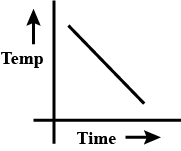
d. 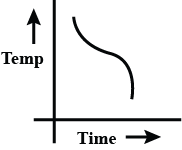
Solution
When expressed in terms of temperature differences, Newton's law (along with a few additional simplifying assumptions including a low Biot number and a temperature-independent heat capacity) yields a simple differential equation that expresses temperature difference as a function of time. The solution to that equation represents a reduction in temperature differential over time that is exponential. Newton's law of cooling is also linked to this signature decay of the temperature difference.
Complete step-by-step answer:
The rate at which an exposed body changes temperature by radiation is roughly proportional to the difference between the object's temperature and its environment, given the difference is slight, according to Newton's law of cooling. The rate of heat loss from a body is directly proportional to the difference in temperature between the body and its surroundings, according to Newton's law of cooling.
It Is given by the formula
dT/dt=k(Tt−Ts)
Tt=temperature of the body at time t and
Ts=temperature of the surrounding,
K = The area and function of the body's surface under consideration determine the positive constant.
Now according to the Newton's law of cooling
⇒ rate of cooling α temperature
θ→ temp
dtdθα(θ−θ0)
dtdθ=α(θ−θ0)(α= constant )
∫θiθ(θ−θ0)dθ=∫0tαdt
⇒θ=θ0+(θ1−θ0)e−αt
From this we deduce the graph is exponential
So, the correct answer is “Option B”.
Note: When the internal thermal resistance inside the material is minimal in contrast to the resistance to heat transfer away from the object's surface (by external conduction or convection), which is the case for which the Biot number is less than about 0.1, simple methods for temporary cooling of an object can be obtained. This condition allows for the assumption of a single, roughly uniform body temperature that varies with time but not with location. (Otherwise, the body will be at a variety of temperatures at any given time.) As time passes, the temperature of this single object can change exponentially.
