Question

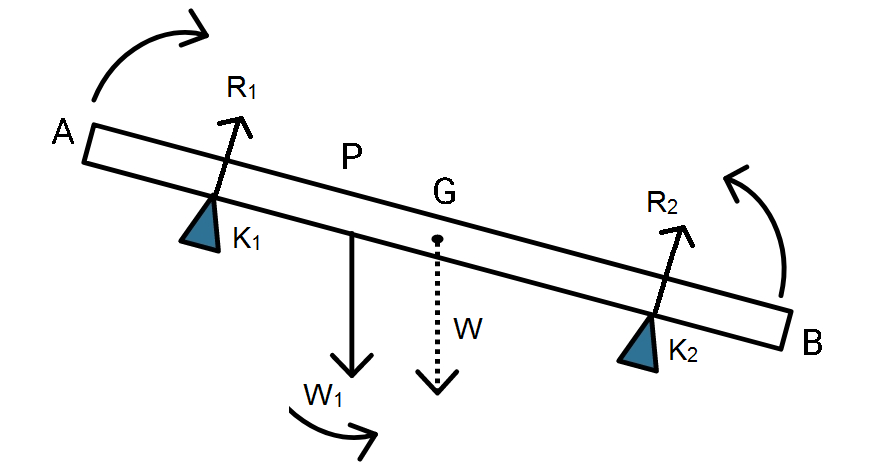
: A metal bar of 70 cm long and 4 kg in mass supported on the two knife edges placed 20 cm from each end. A 6 kg load is suspended at 30 cm from on end. Find the normal reaction at the knife-edge. (Assume it to be of uniform cross section and homogeneous).

A. 59 N at $K_1$ and 39 N at $K_2$
B. 43 N at $K_1$ and 53 N at $K_2$
C. 55 N at $K_1$ and 43 N at $K_2$
D. 43 N at $K_1$ and 55 N at $K_2$

Answer 1

The rod is not affected by the placing of the weight, it lies in equilibrium. Rod does not move up or down, so it follows translational equilibrium. It also doesn't move about an axis, so it has rotational equilibrium.

Complete answer:
We are given the rod length to be 70 cm. Two knife edges are present at a distance of 20 cm from both ends. Now, the weight 4 kg of the rod is acting downwards at a point located at the mid point of the rod as it is the centre of gravity for the rod. So, the distance of both the knife edges from the midpoint is (35-20=) 15 cm. The weight of 6 kg is placed at a distance of (35-30 =) 5 cm from the mid point of the rod.

Now consider the following two equilibriums for the rod:
1. The rod is perfectly balanced on the two edges, it is not moving up or down as a whole (or sideways) so it rests in translational equilibrium. Thus, we can write the sum of concerned forces as:
$R_1 + R_2 - W - W_1 = 0$,
keeping $W_1$ = 6g N, W = 4g N, we can write:
$R_1 + R_2 = 10 \times 9.8 N$ = 98 N.

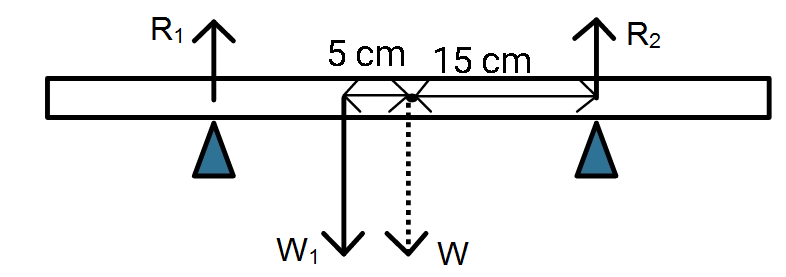
2. As for the case of rotational motion, if there was no $W_1$ and $K_1$ were not in place too, then the rod would have turned in an anticlockwise manner due to a reaction of $R_2$ holding the other end at its place. Similar can be said for the other end too but the motion would have been clockwise for that. As the weight $W_1$ is placed it supports the anticlockwise moment of the rod due to its placement.
In the case of rotational equilibrium,
Clockwise torque = Anticlockwise torque
So, $R_1 \times 15 = W_1 \times 5 + R_2 \times 15$
or, $(R_2 - R_1) \times 15 = 6 \times 9.8 \times 5$
$\implies R_2 - R_1 = 19.6$N.

Thus, using the two equations that we obtained from to equilibrium conditions we can directly calculate by substitution,
$2R_1 = 117. 6 N \implies R_1 = 58.8$N.
Similarly, we can get
$R_2 = 98 - 58.8 = 39.2$N.

So, the correct answer is “Option A”.

Note:
The reaction forces upwards are taken to be positive and wait acting downwards is taken to be negative when writing the equations for equilibrium. Don't forget to multiply the masses by g to get the force due to the weight.