Question

A metal bar $70cm$ long and $4kg$ in mass is supported on two knife edges placed $10cm$ from each end of metal bar. A $6kg$ weight is suspended at $30cm$ from one end. Find the reactions at the knife edges due to these weights. Assume linear mass density of metal bars is constant at all points on metal bars.
A) $45N$ and $43N$
B) $50N$ and $35N$
C) $55N$ and $43N$
D) $54N$ and $30N$

Answer 1

We know every action has an equal and opposite reaction. The reaction at the knife's edges is equal and opposite to the force applied on knife edges by weight of metal bar and suspended weight. When a weight is suspended on rod then the force applied on fixed ends of rod is inversely proportional to the distance of end of rod from the point of suspension of weight.

Complete step by step answer:

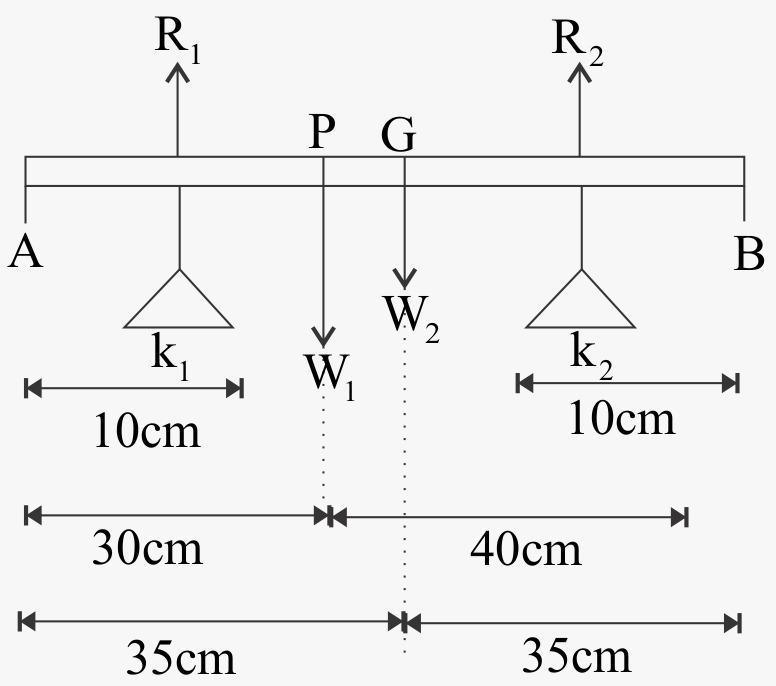
As shown in figure $AB$ is metal bar $70cm$ long and $4kg$ in mass. There are two knife-edges at points $k_1$ and $k_2$ at a distance of $10cm$ from the ends of metal bars.
$G$ is the point of centre of gravity of a metal bar and $P$ is the point of centre of mass of weight suspended on a metal bar.
$W_1$ and $W_2$ are weight of metal bar and suspended weight and, $R_1$, $R_2$ are reactions on edges of knives. We know total weight is equal to total reaction, then
$W_1 + W_2 = R_1 + R_2$ or $W_1 + W_2 - R_1 - R_2 = 0$ -(1)
Rod is in rotational equilibrium means torque due to all forces applied on the metal bar is zero. We check torque on the centre of the rod. $k_1$ and $k_2$ are at a distance of $25cm$ form centre of the bar, $G$ is at centre and $P$ is at $5cm$ from centre.
Then, for rotational equilibrium,
$R_1(k_1G) - R_2(k_2G) - W_2(PG) = 0$ -(2)
Given $W_1 = 4gN$ and $W_2 = 6gN$, where $g$ is acceleration due to gravity of earth and its value is $9.8N/kg$.
Putting these values in equation 1, we get
$R_1 + R_2 = W_1 + W_2 = 10 \times 9.8 = 98N$-(3)
Putting values in equation (2), we get
$0.25R_1 - 0.25R_2 - 0.05W_2 = 0$
$R_1 - R_2 = \dfrac{{W_2}}{5} = \dfrac{{6 \times 9.8}}{5} = 11.76N$ -(4)
After solving equation (3) and (4), we get
$R_1 = 54.88N \simeq 55N$ and $R_2 = 43.12N \simeq 43N$
Hence the correct answer is option C.

Note: Here we know the metal bar is in stable equilibrium then it is in rotational as well as translational equilibrium. Weight of an object is a product of mass of the object and its acceleration. All the questions with similar conditions as the above question are solved by balancing forces and torque on the metal bar or rod.