Question

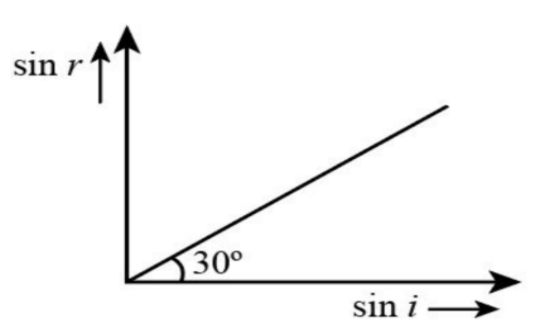
A medium shows relation between i and r as shown. If speed of light in the medium is nc then value of n is

(a) $1.5$
(b) $2$
(c) ${2^{ - 1}}$
(d) ${3^{{{ - 1} {\left/ {\vphantom {{ - 1} 2}} \right.} 2}}}$

Answer 1

From the concept of Brewster’s law of refraction, we can establish a relationship between the slope of the given graph and the polarising angle, which is equal to $30^\circ$. Also, we will use the concept of Snell’s law or the law of diffraction, which gives us the relationship between n and refractive index of the medium of light.

Complete step by step answer:
From the concept of Snell’s law of refraction, we can write:
$n = \dfrac{1}{\mu }$
Here $\mu$ is the refractive index of the medium.
Refractive index can also be written as:

\dfrac{{\sin r}}{{\sin i}} = \dfrac{1}{\mu }\\\ \Rightarrow \dfrac{{\sin i}}{{\sin r}} = \mu \end{array}$$ Substitute $$\dfrac{1}{n}$$ for $$\mu $$ in the above expression. $$\dfrac{{\sin i}}{{\sin r}} = \dfrac{1}{n}$$ We can also write the expression for the slope of the given graph from Brewster’s law. $$\dfrac{{\sin r}}{{\sin i}} = S$$ Here, S represents the slope. Rewriting the above expression, we get: $$\dfrac{{\sin i}}{{\sin r}} = \dfrac{1}{S}$$ Substitute $$\dfrac{1}{n}$$for $$\dfrac{{\sin i}}{{\sin r}}$$ in the above expression. $$\begin{array}{l} \dfrac{1}{n} = \dfrac{1}{S}\\\ n = S \end{array}$$……(1) We can also write the value of slope from the given graph. $$\begin{array}{c} S = \tan 30^\circ \\\ = \dfrac{1}{{\sqrt 3 }} \end{array}$$ Substitute $$\dfrac{1}{{\sqrt 3 }}$$ for S in equation (1). $$n = \dfrac{1}{{\sqrt 3 }}$$ Rewrite the above expression to check which option is correct. $$n = {3^{{{ - 1} {\left/ {\vphantom {{ - 1} 2}} \right.} 2}}}$$ Therefore, if the speed of light is nc, then the value of n is equal to $${3^{{{ - 1} {\left/ {\vphantom {{ - 1} 2}} \right.} 2}}}$$ **So, the correct answer is “Option D”.** **Note:** While writing the slope of the given graph, do not forget to take the inverse of it so that the relationship between slope S and n can be established as a result of which value of n can be determined. Also, do not forget to rewrite the fractional value of n into its simplest form to get the correct answer.