Question

Let $l_1, l_2$ and $l_3$ are the lengths of the tangents drawn from a variable point P to the circle $x^2 + y^2 = a^2; x^2 + y^2 = 2ax$ and $x^2 + y^2 = 2ay$ respectively. The lengths satisfy the relation $l_1^4 = l_2^2 l_3^2 + a^4$. Then the locus of P can be:

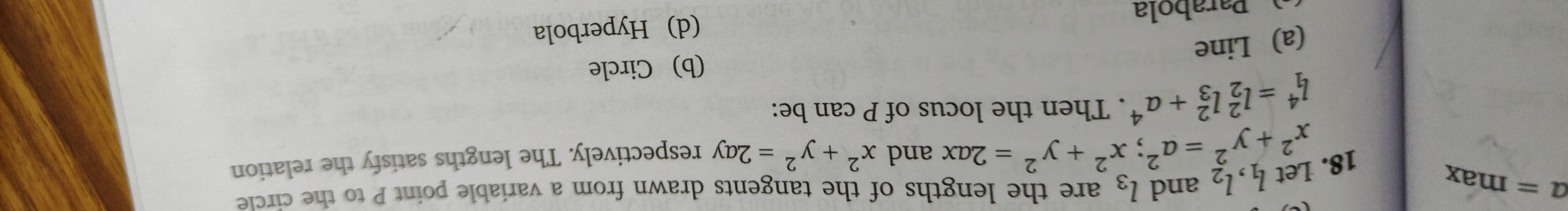
• A. Line
• B. Circle
• C. Hyperbola

Answer 1

Answer: (A), (B)

(a) Line, (b) Circle

Answer 2

Let $P(x, y)$ be the variable point. The square of the length of the tangent from $P(x, y)$ to a circle $S=0$ is given by $l^2 = S(x, y)$.

The equations of the circles are:

1. $C_1: x^2 + y^2 - a^2 = 0 \implies l_1^2 = x^2 + y^2 - a^2$
2. $C_2: x^2 + y^2 - 2ax = 0 \implies l_2^2 = x^2 + y^2 - 2ax$
3. $C_3: x^2 + y^2 - 2ay = 0 \implies l_3^2 = x^2 + y^2 - 2ay$

The given relation is $l_1^4 = l_2^2 l_3^2 + a^4$. Substituting the expressions for $l_i^2$: $(x^2 + y^2 - a^2)^2 = (x^2 + y^2 - 2ax)(x^2 + y^2 - 2ay) + a^4$

Let $X = x^2 + y^2$. The equation becomes: $(X - a^2)^2 = (X - 2ax)(X - 2ay) + a^4$ $X^2 - 2a^2X + a^4 = X^2 - 2aXy - 2aXx + 4a^2xy + a^4$

Canceling $X^2$ and $a^4$ from both sides: $-2a^2X = -2aXy - 2aXx + 4a^2xy$

Assuming $a \neq 0$, we can divide the equation by $-2a$: $aX = Xy + Xx - 2axy$

Substitute $X = x^2 + y^2$ back into the equation: $a(x^2 + y^2) = (x^2 + y^2)y + (x^2 + y^2)x - 2axy$ $a(x^2 + y^2) = (x^2 + y^2)(x + y) - 2axy$

Rearranging the terms: $(x^2 + y^2)(x + y) - a(x^2 + y^2) - 2axy = 0$ $(x^2 + y^2)(x + y - a) - 2axy = 0$

This equation can be factored into two parts. One part leads to $x+y=0$, which is a straight line. The other part leads to $x^2 + y^2 - ax - ay = 0$, which is the equation of a circle.

Thus, the locus of point P is the union of a line and a circle. Therefore, the locus can be a line or a circle.