Question

A massless inextensible string in the form of a loop is placed on a horizontal film of soap solution of surface tension T. If film is pierced inside the loop and it converts into a circular loop of diameter d, then the tension produced in string is :
$\text{A}\text{. }Td$
$\text{B}\text{. }\pi Td$
$\text{C}\text{. }\pi {{d}^{2}}T$
$\text{D}\text{. }\dfrac{\pi {{d}^{2}}T}{4}$

Answer 1

Consider a small arc of the circular loop. Find the force exerted by the solution with the formula of surface tension. Then find the tension force that balances this force by dividing the tension into horizontal and vertical components. Equate the forces and find the value of tension.

Complete step by step answer:
The soap solution will exert forces at every point on the inside and outside circumferences of the string. As a result, the string expands outwards and forms a circular loop. When the string forms a circular loop, it cannot expand further and hence a tension is developed in the string that balances the outward force on the string.
Consider a small arc of the circular loop of length l.

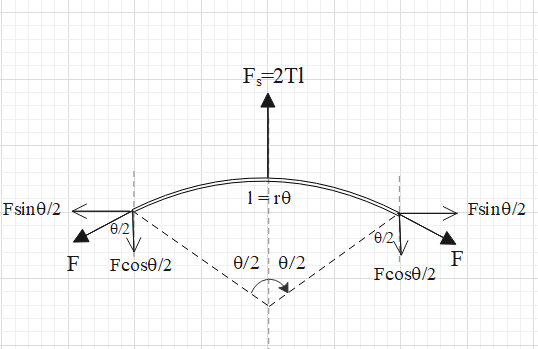
The surface tension T is the defined as the force exerted by the liquid perpendicular to a curve divided by length of the curve.
In this case, the solution exerts force on the two curves of the arc. Hence, the total length is 2l.
Therefore, $T=\dfrac{{{F}_{s}}}{2l}$.
This means that the solution will exert a force equal to $2Tl$ in the upward direction as shown.
Let this arc subtend a small angle $\theta$ and let the tension be F. The tension will pull the arc outwards as shown in the figure.
Resolve the tension F into its horizontal and vertical components as shown. The horizontal component will be $F\cos \dfrac{\theta }{2}$ and the vertical component will be $F\sin \dfrac{\theta }{2}$
Now, the net force in the horizontal direction is ${{F}_{x}}=F\sin \dfrac{\theta }{2}-F\sin \dfrac{\theta }{2}=0$ .
This means that the horizontal components of the tensions at both the ends balanced each other.
Since the loop is in equilibrium, the net force in vertical direction is also zero.
This means that ${{F}_{y}}=2Tl-2F\sin \dfrac{\theta }{2}=0$.
$\Rightarrow 2Tl=2F\sin \dfrac{\theta }{2}$ ….. (i).
Therefore, the vertical components of the tension will balance the force exerted by the solution.
For a small angle, sine of the angle is equal to the angle.
Therefore, $\sin \dfrac{\theta }{2}=\dfrac{\theta }{2}$ .
And from the arc-length formula we get $r\theta =l$, where r is the radius and l is the length of the arc.
And $r=\dfrac{d}{2}$.
Substitute the value of r in the arc length formula.
$\Rightarrow \dfrac{d}{2}\theta =l$
Substitute this value of $\sin \dfrac{\theta }{2}$ and l in (i)
$\Rightarrow 2T\left( \dfrac{d}{2}\theta \right)=2F\dfrac{\theta }{2}$
$\Rightarrow F=Td$.
This means that the tension produced in the string is equal to Td.
Hence, the correct option is A.

Note:
Know that when we say that for a small angle, the sine of the angle is equal to the angle, the angle is measured in radians and not in degrees.
The direction of forces exerted by the solution are radially outwards. Since it is a small arc, we can consider the net force in the upward direction and equal to 2Tl.