Question
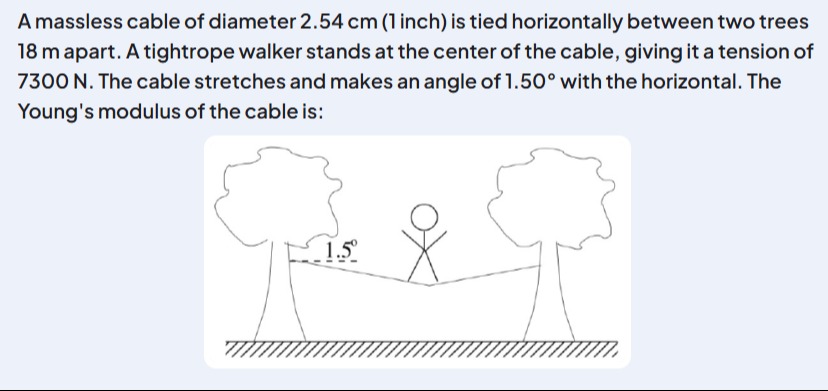
Question: A massless cable of diameter 2.54 cm (1 inch) is tied horizontally between two trees 18 m apart. A t...
A massless cable of diameter 2.54 cm (1 inch) is tied horizontally between two trees 18 m apart. A tightrope walker stands at the center of the cable, giving it a tension of 7300 N. The cable stretches and makes an angle of 1.50° with the horizontal. The Young's modulus of the cable is:
Answer
E≈4.20×1010 Pa
Explanation
Solution
Solution
- Determine the extension:
For one half of the cable, the horizontal distance is 9 m. When stretched, the half‐cable makes an angle θ=1.50∘ with the horizontal so that its actual length becomes
L′=cosθ9.The extension of each half is
δ=L′−9=9(cosθ1−1).With cos(1.50∘)≈0.999657,
δ≈9(1.000343−1)≈9(0.000343)≈0.003087 m.- Calculate the cross‐sectional area A:
The cable’s diameter is 2.54 cm, so its radius is
r=22.54 cm=1.27 cm=0.0127 m.Thus,
A=πr2=π(0.0127)2≈π(0.00016129)≈0.0005067 m2.- Apply Hooke’s law to relate stress and strain:
The stress in the cable is
σ=AT,and the strain in one half is
ϵ=9δ.The Young's modulus is given by
E=ϵσ=δ/9T/A=Aδ9T.- Substitute the known values:
Given T=7300N,
E=0.0005067×0.0030879×7300≈1.565×10−665700≈4.20×1010Pa.Explanation (Minimal):
- Compute extension δ=9(1/cos1.5∘−1)≈0.003087 m.
- Find cross-sectional area A=π(0.0127)2≈0.0005067 m².
- Use E=Aδ9T.
- Substitute T=7300 N and compute E≈4.20×1010 Pa.
