Question

A massless bucket is initially at rest next to one end of a chain that lies in a straight line on the floor, as shown in Fig. The chain has uniform mass density $\lambda(kg/m)$. You push on the bucket (so that it gathers up the chain) with the force F(t) that gives the bucket and whatever chain is inside, a constant acceleration a at the times. 't' is time. There is no friction between the bucket and the floor. Then the work done by F(t) upto time t is

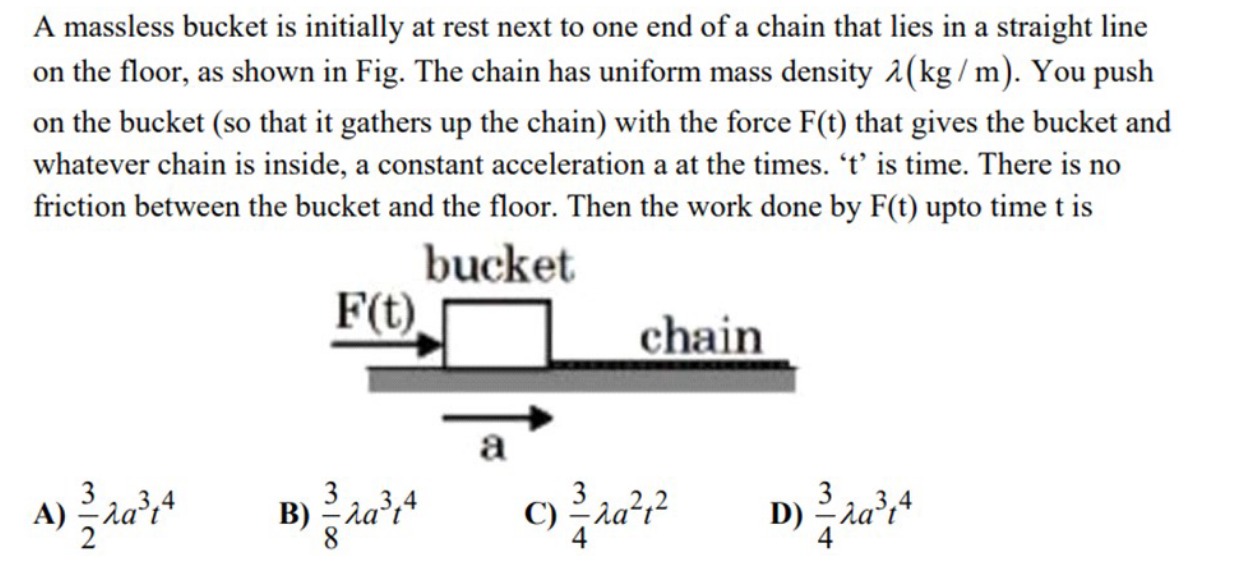
• A. $\frac{3}{2}\lambda a^3t^4$
• B. $\frac{3}{8}\lambda a^3t^4$
• C. $\frac{3}{4}\lambda a^2t^2$
• D. $\frac{3}{4}\lambda a^3t^4$

Answer 1

Answer: (B)

$\displaystyle \frac{3}{8}\lambda a^3t^4$

Answer 2

Let the bucket pull chain at constant acceleration $a$. At time $t$:

• The bucket's displacement is $$s(t)=\frac{1}{2}at^2,$$ so the mass collected is $$m(t)=\lambda s(t)=\frac{1}{2}\lambda at^2.$$
• The velocity of the bucket is $$v(t)=at.$$

For a variable-mass system, the net force is given by

$$F = \frac{d(mv)}{dt} = m\,a + v\,\frac{dm}{dt}.$$

Since

$$\frac{dm}{dt} = \lambda \frac{ds}{dt} = \lambda v = \lambda a t,$$

substitute to obtain:

$$F = \left(\frac{1}{2}\lambda at^2\right)a + (at)\left(\lambda at\right)= \frac{1}{2}\lambda a^2t^2 + \lambda a^2t^2 = \frac{3}{2}\lambda a^2t^2.$$

The instantaneous power is

$$P = Fv = \frac{3}{2}\lambda a^2t^2\cdot (at)=\frac{3}{2}\lambda a^3t^3.$$

Thus, the work done up to time $t$ is

$$W = \int_0^t P\,dt = \int_0^t \frac{3}{2}\lambda a^3\tau^3\,d\tau = \frac{3}{2}\lambda a^3\cdot\frac{t^4}{4} = \frac{3}{8}\lambda a^3t^4.$$