Question
Question: A massless block attached to a spring, pulled by a constant horizontal force,is kept on a smooth sur...
A massless block attached to a spring, pulled by a constant horizontal force,is kept on a smooth surface as shown in Fig. initially ,the spring is in its natural length . Then the maximum positive work that the applied force F can do is ( given that spring does not break)
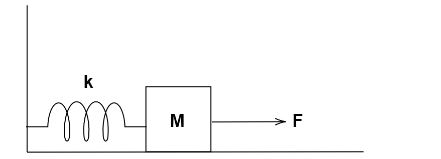
A. kF2
B. k2F2
C. ∞
D. 2kF2
Solution
To solve the given question we use the concepts of work, potential energy and displacement. We are given the force constant of the spring and force applied on the block. Using these we can find displacement. Work done by spring to be positive, should make the block displace in the direction of force i.e. right. Now we put the value of displacement in the potential energy formula which is indeed work done by spring.
Formulae used-
U=2kx2
⇒F=kx
where x is the displacement of a block and Spring constant is given as k.
Complete step by step answer:
We are given constant force applied on the block as F. Spring constant is given as k
Force in spring =constant force applied on block (as both act in opposite directions and no other forces are acting horizontally on block)
F=kx
Now we can write maximum displacement as x=kF. As we know The Work on a body is stored as converted to energy. There are two main types of mechanical energy namely, kinetic and potential energy. If the body has no velocity then the work done on it is converted entirely to potential energy. work done in stretching a spring is stored as the elastic potential energy given by the equation,
U=2kx2=W
Now taking the value of x we derived x=kF in the above equation we get
\Rightarrow W = \dfrac{{k{{\left( {\dfrac{F}{k}} \right)}^2}}}{2} \\\ \Rightarrow W = \dfrac{{k{F^2}}}{{2{k^2}}} \\\ \Rightarrow W = \dfrac{{{F^2}}}{{2k}}$$ Thus, the maximum positive work that the force can do is $$ \therefore W = \dfrac{{{F^2}}}{{2k}}$$ **Therefore, the correct answer is option $${\text{D}}$$.** **Note:** When inelastic deformation has not occurred, the work done is equal to the accumulated elastic potential energy. The work also can be visualized because of the area under the force curve. The energy is stored until the energy is removed and therefore the material returns to its original form.