Question

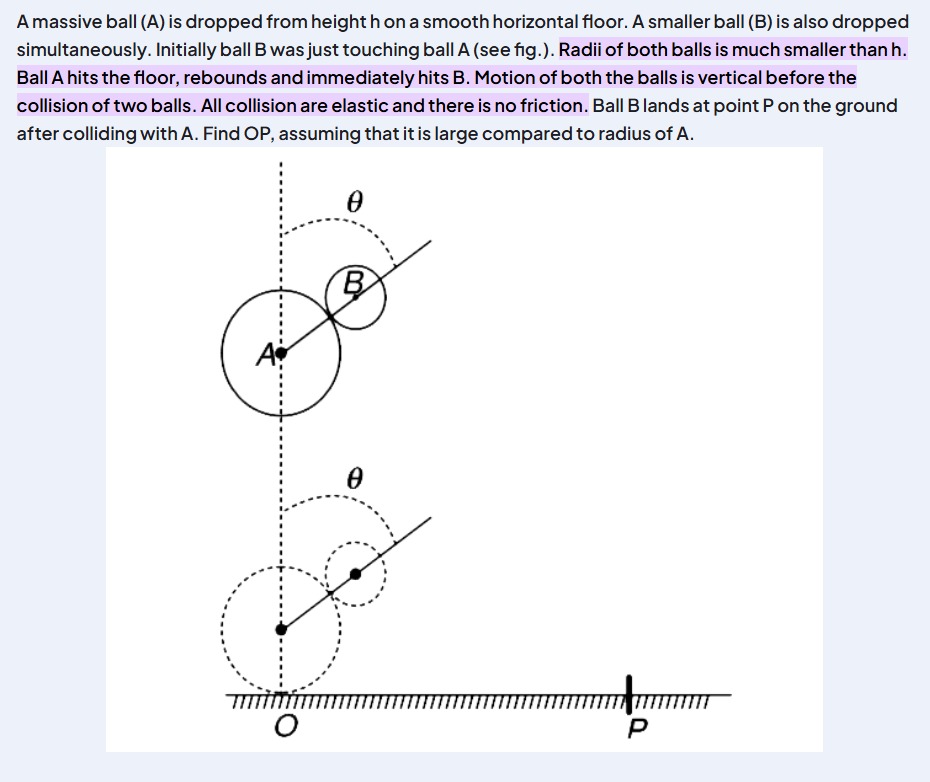
A massive ball (A) is dropped from height h on a smooth horizontal floor. A smaller ball (B) is also dropped simultaneously. Initially ball B was just touching ball A (see fig.). Radii of both balls is much smaller than h. Ball A hits the floor, rebounds and immediately hits B. Motion of both the balls is vertical before the collision of two balls. All collision are elastic and there is no friction. Ball B lands at point P on the ground after colliding with A. Find OP, assuming that it is large compared to radius of A.

Answer 1

8h

Answer 2

The solution involves analyzing the motion of the balls before and after the collision between ball A and ball B.

1. Motion before collision with the floor: Both balls are dropped from height h. Their initial velocities are 0. Just before hitting the floor, the velocity of ball A is $\sqrt{2gh}$ downwards. At the same time, ball B is also at a height just above the floor and has a velocity of $\sqrt{2gh}$ downwards.

2. Collision of ball A with the floor: The collision is elastic, so ball A rebounds with the same speed, i.e., its velocity immediately after hitting the floor is $\sqrt{2gh}$ upwards.

3. Collision of ball A and ball B: Immediately after A rebounds from the floor, it collides with ball B. At this moment, ball A is moving upwards with speed $v_A = \sqrt{2gh}$, and ball B is moving downwards with speed $v_B = \sqrt{2gh}$. The collision is oblique and elastic. Ball A is massive compared to ball B ($m_A \gg m_B$). The line connecting the centers of A and B at the moment of collision makes an angle $\theta$ with the vertical.

   Let the upward direction be positive. Just before the collision of A and B, the velocity of A is $\vec{v}_{A,i} = \sqrt{2gh} \hat{j}$ and the velocity of B is $\vec{v}_{B,i} = -\sqrt{2gh} \hat{j}$. The line of centers makes an angle $\theta$ with the vertical. Let the unit vector along the line of centers be $\hat{n}$. From the figure, if the center of B is to the right of A, $\hat{n} = \sin\theta \hat{i} + \cos\theta \hat{j}$. The unit vector perpendicular to the line of centers is $\hat{t} = \cos\theta \hat{i} - \sin\theta \hat{j}$.

   The components of initial velocities along and perpendicular to the line of centers are: $v_{A,i,||} = \vec{v}_{A,i} \cdot \hat{n} = \sqrt{2gh} \cos\theta$ $v_{A,i,\perp} = \vec{v}_{A,i} \cdot \hat{t} = -\sqrt{2gh} \sin\theta$ $v_{B,i,||} = \vec{v}_{B,i} \cdot \hat{n} = -\sqrt{2gh} \cos\theta$ $v_{B,i,\perp} = \vec{v}_{B,i} \cdot \hat{t} = \sqrt{2gh} \sin\theta$

   In an elastic collision with no friction, the velocity components perpendicular to the line of centers are unchanged: $v_{A,f,\perp} = v_{A,i,\perp} = -\sqrt{2gh} \sin\theta$ $v_{B,f,\perp} = v_{B,i,\perp} = \sqrt{2gh} \sin\theta$

   For the collision along the line of centers, using the elastic collision formulas and the approximation $m_A \gg m_B$: $v_{A,f,||} \approx v_{A,i,||} = \sqrt{2gh} \cos\theta$ $v_{B,f,||} \approx 2v_{A,i,||} - v_{B,i,||} = 2(\sqrt{2gh} \cos\theta) - (-\sqrt{2gh} \cos\theta) = 3\sqrt{2gh} \cos\theta$

   The final velocity of ball B is $\vec{v}_{B,f} = v_{B,f,||} \hat{n} + v_{B,f,\perp} \hat{t}$. $\vec{v}_{B,f} = (3\sqrt{2gh} \cos\theta) (\sin\theta \hat{i} + \cos\theta \hat{j}) + (\sqrt{2gh} \sin\theta) (\cos\theta \hat{i} - \sin\theta \hat{j})$ $\vec{v}_{B,f} = (3\sqrt{2gh} \sin\theta \cos\theta + \sqrt{2gh} \sin\theta \cos\theta) \hat{i} + (3\sqrt{2gh} \cos^2\theta - \sqrt{2gh} \sin^2\theta) \hat{j}$ $\vec{v}_{B,f} = (4\sqrt{2gh} \sin\theta \cos\theta) \hat{i} + (\sqrt{2gh} (3\cos^2\theta - \sin^2\theta)) \hat{j}$ $\vec{v}_{B,f} = (2\sqrt{2gh} \sin(2\theta)) \hat{i} + (\sqrt{2gh} (4\cos^2\theta - 1)) \hat{j}$

   The horizontal component of velocity of B is $v_{Bx} = 2\sqrt{2gh} \sin(2\theta)$. The vertical component of velocity of B is $v_{By} = \sqrt{2gh} (4\cos^2\theta - 1)$.

4. Projectile motion of ball B: Ball B starts its motion from a height very close to the ground (approximately 0) with initial velocity $\vec{v}_{B,f}$. The horizontal range OP is given by $R = v_{Bx} t$, where $t$ is the time of flight. The time of flight is determined by the vertical motion: $0 = v_{By} t - \frac{1}{2} g t^2$. $t = \frac{2v_{By}}{g} = \frac{2 \sqrt{2gh} (4\cos^2\theta - 1)}{g}$. For the ball to land at a point P on the ground, it must have a positive time of flight, which requires $v_{By} > 0$. Thus, $4\cos^2\theta - 1 > 0$, so $\cos\theta > 1/2$, which means $0 \le \theta < \pi/3$.

   The range is $OP = v_{Bx} t = (2\sqrt{2gh} \sin(2\theta)) \times \frac{2\sqrt{2gh} (4\cos^2\theta - 1)}{g}$ $OP = \frac{4 \times 2gh \sin(2\theta) (4\cos^2\theta - 1)}{g} = 8h \sin(2\theta) (4\cos^2\theta - 1)$.

5. Finding the angle $\theta$: Assuming $\theta = \pi/4$ is the intended angle of collision.

   Horizontal velocity of B after collision: $v_{Bx} = 2\sqrt{2gh} \sin(2 \times \pi/4) = 2\sqrt{2gh} \sin(\pi/2) = 2\sqrt{2gh}$. Vertical velocity of B after collision: $v_{By} = \sqrt{2gh} (4\cos^2(\pi/4) - 1) = \sqrt{2gh} (4(1/2) - 1) = \sqrt{2gh}$. Time of flight: $t = \frac{2v_{By}}{g} = \frac{2\sqrt{2gh}}{g} = 2\sqrt{\frac{2h}{g}}$. Horizontal range: $OP = v_{Bx} t = (2\sqrt{2gh}) (2\sqrt{\frac{2h}{g}}) = 4 \sqrt{2gh \times \frac{2h}{g}} = 4 \sqrt{4h^2} = 4(2h) = 8h$.